VIDEO TRANSCRIPT

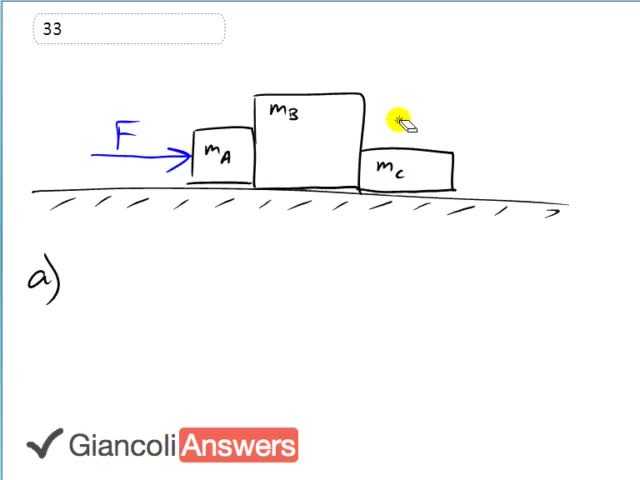
We have to draw a free body diagram for each of these blocks. We know that there’s an external force pushing on block a which willing turn push on block b which in turn pushes on block c and there’s going to be a reaction-reaction pairs between each of these contact points. Block a pushes on b and then block b will in turn push back on a with the same magnitude force. So we have ‘m’ times ‘a’ with gravity going down and normal force going up. It’ll have the external force pushing it to the right and it will have the reaction force, the force on block a due to block b. Block b will in turn push back on a. The free body diagram for mass b will look like this. It will have normal force upwards for block b and it’ll have gravity downwards. There will be the force on block b due to block a that’s due to the contact here. And then block b is stuck in the middle so it also is experiencing a force on block b due to block c in reaction to block b pushing on block c. So we have the force on block b due to block c and there’s a free body diagram. And then block c is going to have gravity, normal force and only one horizontal force. So this is a normal force in block c. gravity on block c and the force on block c due to block b. That’s part a done. In part b we have to find the acceleration of the system. From the perspective of this external force, you can imagine a single mass of mass a, b and c put together. So this could be our picture for the whole system from the perspective of the external force ‘F’ and that being the case we can say ‘F’ which is the net force in this case is mass times acceleration where ‘m' is the total mass of everything. So we have ‘ma’ plus ‘mb’ plus ‘mc’ times the system’s acceleration and then we’ll solve for that acceleration by dividing by the sum of the masses. So acceleration is: force divided by ‘ma’ plus ‘mb’ plus ‘mc’. This is our answer to part b. In part c we have to find the net force on each block. So the net force on block a is going to be mass a times acceleration, that’s Newton’s second law, and so we just multiply that by ‘ma’ to get our answer. So we have the external force times ‘ma’ divided by ‘ma’ plus ‘mb’ plus ‘mc’. And then the same logic applies to the other two blocks. So force b net is mass b times acceleration so that’s ‘mb’ times ‘F’ divided by ‘ma’ plus’ mb’ plus ‘mc’. And then net force on block c is ‘mc’ times ‘a’ which is ‘mc’ times ‘F’ over ‘ma’ plus ‘mb’ plus ‘mc’. Part d. We have to find the force of contact that each block exerts on its neighbor. So consider block a, Newton's second law horizontally speaking for block a would be that the external force ‘F’ to the right minus the force on a due to block b equals mass a times acceleration so we have ‘F’ minus ’FAB’ equals ‘m’ times ‘a’. And looking at the free body diagram that is true because we have ‘F’ to the right, ‘FAB’ to the left and that is going to equal mass times acceleration. So let’s solve for ‘FAB’ by adding it to both sides and then subtract ‘ma’ times ‘a’ from both sides as well. We end up with ‘FAB’ equals ‘F’ minus ‘ma’ times ‘a’. So we have ‘ma’ times ‘F’ over ‘ma’ plus 'mb’ plus ’mc’. So we have ‘F’ times ‘ma’ plus ‘mb’ plus ‘mc’ minus ‘ma’ times ‘F’ all over ‘ma’ plus ‘mb’ plus ‘mc’. And when we expand we have another term ‘mAF’ will be cancelling leaving us on the top with only ‘F’ times ‘mb’ plus ‘F’ times ‘mc’ over the sum of the masses. Factoring out the ‘F’: ‘F’ times ‘mb’ plus ‘mc all over ‘ma’ plus ‘mb’ plus ‘mc’. This is the contact force between blocks a and b so that’s ‘FAB’. Continuing on we have a block b. There are two forces ’FBA’ and ’FBC’ going horizontally and so the right one minus the left one will equal its acceleration. So there’s the force on block b due to the first block a to the right minus the force on block b due to block c which is to the left equals ‘mb’ times ‘a’. And we know that this force ’FBA’ is equal in magnitude to force ’FAB’, we know it and so that means this is the one we’re trying to find. So let’s solve for it: ’FBC’ equals ’FBA’ minus ‘mb’ times ‘a’, so ’FBC’ equals ‘F’ times ‘mb’ plus ‘F’ times ‘mc’ over ‘ma’ plus ‘mb’ plus ‘mc’ and that is: minus ‘mb’ times ‘a’ where ‘a’ is ‘F’ over ‘ma’ plus ‘mb’ plus ‘mc’ and these denominators are the same which means we can combine the numerators and the ‘mb’ times ‘F’ terms will cancel leaving us with an answer that the contact force between blocks b and c is: magnitude ‘F’ times ‘mc’ over ‘ma ‘ plus ‘mb’ plus 'mc’. And the block c we don’t have to think about too much because the magnitude of the force on block c due to b is the same in size to the force on block b due to c. Part e says do all the stuff again with numbers. So we have acceleration is: force divided by ‘ma’ plus ‘mb’ plus ‘mc’. So that’s ninety six newtons divided by three times twelve kilograms because they’re all the same mass so that’s two point six seven meters per second squared. Then we find the contact forces. We have the contact force between a and b is going to be ninety six newtons times two times twelve kilograms divided by three times twelve kilograms giving us an answer of sixty four newtons is the contact force between blocks a and b. And then between blocks b and c we have ninety six newtons times twelve kilograms divided by three times twelve kilograms giving us the contact force between blocks b and c of thirty two newtons. And we can also talk about the net forces, net force in block a was ‘ma’ times ‘a’ which is twelve point zero kilograms times two point six six six six meters per second squared which gives us thirty two point zero newtons is the net force on block a. But since all the masses are the same and the accelerations are all the same when we write this Newton's second law expression for each of blocks b and c we’ll be using ‘mb’ and ‘mc’ and those masses are all the same and since it’s all accelerating together ‘a’ is the same for everything so everything experiences the same net force: ‘Fb’ net equals ‘Fc’ net which equals ‘Fa’ net which is thirty two point zero newtons. And then it asks us to do a realty check. Let’s look at the acceleration one. It says that as the external applied force increases then the acceleration increases. Well that’s good because that’s constant with our experience. You can imagine more force would mean more acceleration and the equation says the same thing so it must be right. And then the denominator says when the blocks are really heavy for a given force that’s constant increasing the mass the blocks will decrease the acceleration. And that’s just saying the obvious. It is harder to move really massive blocks.