VIDEO TRANSCRIPT

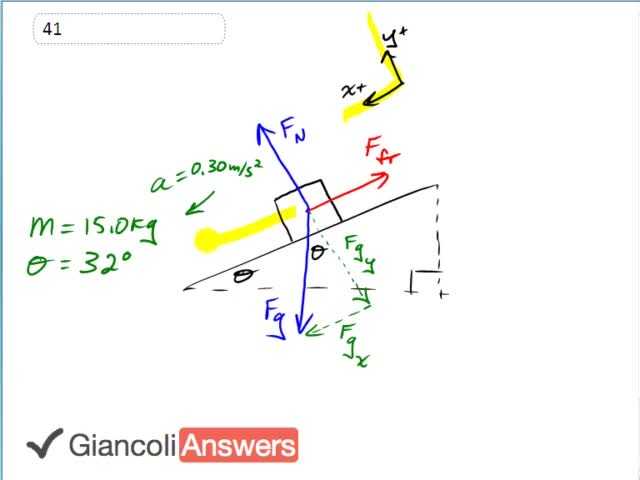
This box is accelerating down the incline and we’ll choose our coordinate system this way so that we have a positive direction of acceleration. And we know that the X-component of gravity is winning here it’s bigger than the force of friction and we are going to say that algebraically. So we’ve written down the stuff that we know about the question and drawn a free body diagram and these are the good things you need to do when answering any question really. So we have the force of gravity which we’ll have as positive because of the way we have defined our coordinate system minus the force of friction equals mass times acceleration. Those are the only forces in the X-direction and the acceleration is zero point three meters per second squared down the ramp. Our job is to figure out the friction force and we’ll add ‘Ffr’ to both sides and them move ‘m’ times ‘a’ to the left side and then flip the sides around we end with force of friction equals ‘Fgx’ minus ‘ma’. ‘Fgx’ is the opposite leg of the gravity force triangle and so we use sine to get it. So we’ll say: force of friction is ‘Fg’ sine theta minus ‘m’ times ‘a’. And ‘Fg’ is ‘mg’ and so force of friction is ‘mg’ times sine theta minus ‘ma.’ We can factor out the ‘m’ so we have ‘m’ times ‘g’ sine theta minus ‘a’ and then we can substitute in values to get our answer which is fifteen kilograms times nine point eight meters per second squared times sine of thirty degrees minus zero point eight meters per second squared and that gives seventy three point three nine eight which we’ll write as seventy three newtons. That’s the friction force impeding the acceleration of the block. It would accelerate faster were it not for the friction force. For the coefficient of kinetic friction we know that the friction equals that coefficient times ‘Fn’ and ‘Fn’ is equal to the Y-component of gravity since there is no acceleration into or out of perpendicularly to the ramp so ‘Fn’ is equal of ‘Fgy’ and ‘Fgy’ is the adjacent leg of that triangle so we have ‘μk’ times ‘mg’ cosine theta. And now we’ll solve for ‘μk’ by dividing both sides by ‘mg’ cosine theta and now solving for ‘μk’: the coefficient for kinetic friction equals the friction force divided by ‘mg’ cosine theta which is seventy three point three nine eight newtons divided by fifteen kilograms times nine point eight meters per second squared times cosine thirty two giving us a coefficient of kinetic friction of zero point five nine. In the 5th Edition the mass is eighteen kilograms and the angle is thirty seven degrees and the acceleration is zero point two seven zero meters per second squared and we’ll substitute those numbers down here and that gives a force of friction in the 5th Edition of one hundred and one newtons and giving you a coefficient of kinetic friction in the 5th Edition of zero point seven one nine.