VIDEO TRANSCRIPT

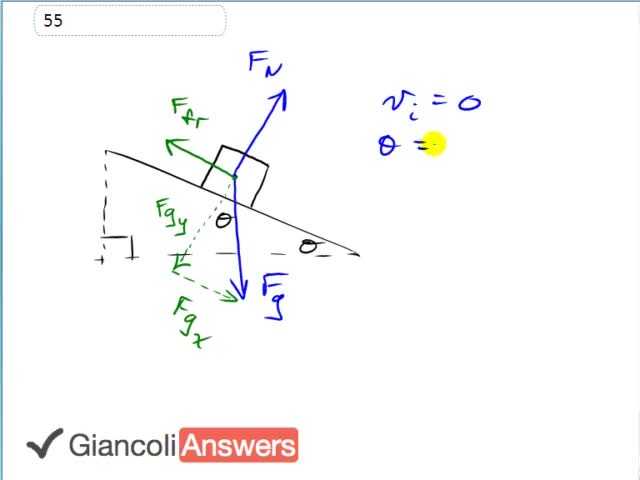
This mass is released with an initial speed of zero and it’s on an incline of angle thirty seven degrees and the questions are: what friction force must be impeding its motion knowing that the acceleration is only zero point two seven zero meters per second squared, it would otherwise be bigger if there was no friction? And the question also is what is the coefficient of friction? So we use Newton’s second law to answer part a, we’ll say that ‘Fgx’ minus the friction force that equal ‘ma’ and we know that the friction force is ‘Fgx’ minus ‘ma’, simplifying and substituting for ‘Fgx’ and instead called it ‘mg’ sine theta because ‘Fgx’ is the opposite leg of this gravity force triangle minus ‘ma’ so we have the friction force is ‘m’ times ‘g’ sine theta minus ‘a’ and we’ll substitute the numbers: it’s eighteen kilograms times nine point eight meters per second squared times sine thirty seven minus zero point two seven zero meters per second squared then all of that equals one hundred and one newtons as the friction force that’s preventing this box from accelerating at a faster rate. So we know that the friction force equals ‘μk’ times ‘FN’ and we’ll use this to figure out the coefficient of friction, ‘FN’ is the Y-component of gravity since there is no acceleration perpendicular to the ramp this ‘FN’ must be equal to the Y-component of gravity. And then we know that that’s the adjacent leg of that gravity force triangle so we have ‘μk’ times ‘mg’ cosine theta is going to be our friction force. So we can solve for ‘μk’ divide both sides by ‘mg’ cosine theta solving for ‘μk’. Let’s substitute in numbers: we have a hundred and one point three before rounding for the friction force divided by eighteen point zero kilograms times nine point eight newtons per kilogram times cosine of thirty seven. This gives a coefficient of friction of zero point seven one nine.