VIDEO TRANSCRIPT

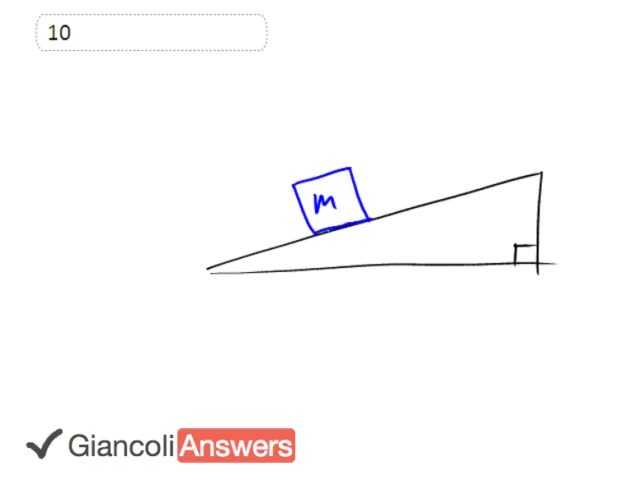
So we have this car of mass 'm' say and it's on this incline and it's going to be pushed up this distance 'd' along this incline and for part A of this question with no friction we'll just need to know what this height is and then we'll multiply gravity by that height and we'll get our answer for the work done in the case with no friction. The well we know that with this angle theta in there that's the angle of inclination of this ramp. We know that the sine theta is the opposite height divided by the hypotenuse which is 'd' for distance with length of the ramp. And we could solve for 'h' and say that it's 'd' sine theta. And then we'll say that the work done by the applied force which is pushing the mass up the ramp is the applied force it's going to equal 'mg' times 'h.' It's only the component of this applied force which is along the, the height that is going to matter and this works out for us.

Whenever you're lifting something regardless of whether it's along a ramp or straight up the work done is… by the lifting force is going to be the weight times the height that it's raised. The path that it takes to get to that height doesn’t matter. So we have 'mg' times 'd' sine theta substituting for 'h' and this gives us 950 kilograms times 9.8 newtons per kilogram times 810 meters is the length of the ramp times sine of 9 degrees. These numbers are different in the fifth edition but we'll talk about that at the end. So we have 1.2 times 10 to the 6 joules of work done by the applied force when there's no friction. In part B it's a different story. Let's take this picture down there. We're going to add some friction force factors onto this picture now. Well it's going to be important to label the normal force. It was there before too but we didn’t bother labeling it because it wasn’t important. So this is the normal force and we have gravity straight down and there's friction straight backwards against the direction of motion. And there's also a component of gravity pointing down the ramp as well. [???] to tell what color we should make that let's make that black. So that black dotted line is the component of gravity along the ramp.

So our coordinate system is like this with 'x' down the ramp and then we have a component of gravity perpendicular to the ramp that's 'Fgy.' Okay since this car is going to be moving at constant speed we can say that the applied force equals the total friction force plus 'x' component of gravity. So the total force is going one direction as equal the total force is going the opposite direction in order to have constant speed. You know what actually I'm going to flip this coordinate system around this is really a minor point it's the age old negative sign issue. Let's put 'x 'positive up the ramp so that we end up getting a positive work it just feels better that way. So we have this applied force equals the total forces that are going down the ramp in order to, to go any further we need to figure out what is this friction force and gravity is fairly straight forward. But the friction well we need to find the normal force and then multiply that by mu in order to get the friction. We have this angle theta in here and we can say that friction force equals mu 'fn' and we can also say that the normal force equals the 'y' component of gravity because there's no acceleration on this line. So the normal force equals the 'y' component of gravity. And say 'f' normal 'Fgy', 'Fgy' is this portion here it's the adjacent leg of that triangle with respect to theta. So we use cosine so we have 'Fg' cos theta or better written as 'mg' cos theta. So here's the normal force

And so then we can say that friction force is going to be mu times that result for the normal force. So we have mu times 'mg' cos theta. The 'x' component of gravity see we're figuring out both of these terms in this formula up here this is the newtons second law. We can say that the 'x' component of gravity is going to be it's the opposite leg of this triangle, opposite to theta. And so we'll say that that's sine. So we have 'mg' times sine theta and substituting for both of these into this formula. We'll say that the applied force equals mu 'mg' cos theta plus 'mg' sine theta. And the work done by the applied force which is the question here is the applied force times 'd' the length of the ramp. We're not going to be using the height in this case instead we're going to use the length of the ramp because, because there's friction involved. Friction is acting along the ramp only and well I mean it has components that are along 'h' as well but friction complicates things and we need to consider the distance along the ramp because that's the same direction as friction. It's a non conservative force is another way to say it and so the path you take when there's friction involved will change the amount of work done. Whereas for a conservative force like gravity it's path independent. So we could just use 'h' but not the case with friction, friction makes things a little bit trickier. So we have to use the actual path that it's going which is along the ramp. So we have 'd' times this applied force so factoring out the 'mg' we have mu cos theta plus sine theta here then we'll substitute the numbers and get our answer we have 810 meters is the length of the ramp 950 kilograms 9.8 newtons per kilogram 0.25 is the coefficient of friction times cosine of 9 degrees and plus sine of 9 degrees and that all equals SOLUTION joules which is a little bit more than twice as much as the answer for part A when there is no friction. So friction makes a big difference, let's talk about the fifth edition alterations to the numbers. The concept is the same but in part A we have a 1,000 kilogram car instead of 950 and the length of the ramp is 300 meters and it's inclined at 17½ degrees. So for the fifth edition the answer is instead 8.8 times 10 to the 5 joules of work done by the applied force when there's no friction and down here we have 300 meters 1,000 kilograms and coefficient of friction is the same at 0.25 but the angle is 17½ and we take the side of 17½ as well. Okay and this gives a fifth edition answer of SOLUTION joules of work done by the applied force.