VIDEO TRANSCRIPT

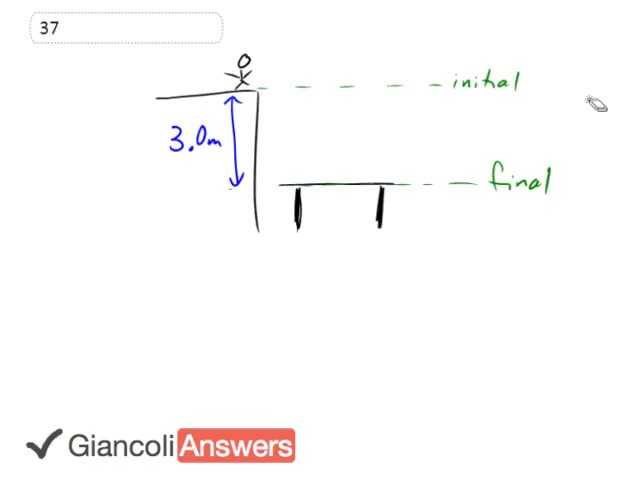
For part A of this question we’re going to say that the top of the cliff is the initial position and the just where they begin to contact the trampoline which is this thing, that we’re going to call that the final position and we’re going to measure our height up on the cliff with respect to the final position with respect to the top of the trampoline, that’s a convenient place to choose our reference point because that means the potential energy final will be zero. So we’re going to start by saying that the potential energy initial plus kinetic energy initial has to equal the potential energy final plus the kinetic energy final. It’s another way of saying conservation of mechanical energy. The initial potential energy is ‘mg’ times the height of the trampoline and the initial kinetic energy is one half ‘mvi’ squared, he lifts off with a certain speed and so we need some kinetic energy initially. Potential energy final is zero because there is no height and kinetic energy final is one half ‘mvf’ squared where ‘vf’ is what we have to find. So we can say one half ‘mvf’ squared where we’re plugging into this expression now, one half ‘mvf’ squared equals the potential energy initial plus the kinetic energy initial and multiplying everything by two and then cancelling the ‘m’s cancel, cancel, cancel. I’m taking the square root of both sides also gives us the ‘ef’ is the square root of ‘2gh’ plus ‘vi’ squared. Substituting in numbers let me get the square, ‘vf’ is the square root of 2 times 9.8 metres per second squared times height of cliff above the top of the trampoline plus 5.0 metres per second that’s the initial speed that he launched off the top of the cliff. And this gives 9.154 metres per second and we should have two sick figs for part A and the answer is 9.2 metres per second that’s our part A answer. Same answer for both the fifth and the sixth editions.

Part B there’s going to be a difference between the fifth and sixth editions we’ll look into that, in this part we need to slightly different picture, we’re going to…here’s the here’s the trampoline and the guy is going to be making a dent on the trampoline because he’s squished down and he is going to go down this far we’ll call that distance ‘x’ here’s the guy…here’s the cliff that he jumped off of…okay and we’ll start by saying the same thing we said before that potential energy initial plus kinetic energy initial equals potential energy final plus kinetic energy final. We can make some simplifying assumptions here, we’re going to say that there’s no kinetic energy in the end because when it gets to the, the deepest depression of this trampoline he’ll stop and then start to come up. So there’s no kinetic energy in the final position so lets just be really clear. This is the final position there and…the top of the trampoline is the initial position for this part B. And there’s no potential energy initially if we’re going to be measuring with respect to this initial reference point, this is our reference point, then there’s no potential energy initial. Now there’s two ways to do this question we’re going to do it the, the best way the most sophisticated way, you could make an assumption that this change in gravitational potential from the top of the trampoline to the point of greatest depression is negligible in which case this question will be pretty simple as far as the algebra goes. But we’re going to actually take it into account just to, to have fun and use a quadratic equation and get the best answer, okay. So the, that means that the final potential energy is not going to just be the elastic potential in the trampoline which is one half ‘kx’ squared. But there’s going to be a reduction in gravitational potential cause he’s gone down so we have minus ‘mgx’ since I have the minus sign in the formula here, that means that this ‘x’ is going to be positive it’s just the it’s a magnitude of its is he’s changing position.

The initial kinetic energy is one half ‘mvi’ squared where we found ‘vi’ from part A, this is the, this is the ‘vf’ of part A, ‘vf’ of part A is the initial speed in this part. So we have one half ‘mvi’ squared equals one half ‘kx’ squared minus ‘mgx’ and we’ll multiply everything by two…and then take the square root of both sides, actually no we’ll just multiply everything by two and then get everything on the same side. So I’m actually going to move this over there…so we have ‘kx’ squared minus ‘mgx’ minus that’s it, two there minus ‘mv’ initial squared okay, and also flip both sides around so that we have the unknowns on the left. This is a quadratic equation for the variable ‘x’ if you, you recall your quadratic formula if you’re having a quadratic with the form ‘ax’ squared plus ‘bx’ plus ‘c’ equals zero I’ll go through this in too much detail but just enough to say that a solution to that is ‘x’ equals negative ‘b’ plus or minus ‘b’ squared minus ‘4ac’ over ‘2a’. So we’re keeping that in mind as we do the quadratic formula here, I’m not going to substitute into the quadratic formula cause that’s a lot of writing and a little tedious but I will write down the numbers that actually go in to this expression so lets do that. So we have 6.2 times 10 to the 4 Newton’s per metre that’s the spring constant times ‘x’ squared that’s ‘a’ in the quadratic formula and then minus two times 65 kilograms times 9.8 Newton’s per kilogram times ‘x’ minus 65 kilograms is the mass of the jumper times the speed that we calculated from part A 9.154 metres per second.

And when you use the quadratic formula you get ‘x’ is 0.3068 or negative 0.286 and the numbers both the magnitudes both are really close so they both seem reasonable and the question will be shall we have the positive or negative? And the answer is we’ll take the positive one because of the way I set up the equation initially, initially I said that…’x’ is going to be a magnitude because we have accounted for the fact that’s losing our potential energy with the negative sign and explicitly in to the formula. And so for that reason we’re going to say ‘x’ is positive. If you had put a plus sign here you’d still get the answer right but you’d end up with an answer positive 0.268 and negative 0.3068 and have to realize that ‘x’ is negative if you have a plus sign here. So the, the trampoline gets squished down by 31 centimetres, now for the fifth edition there’s a couple of changes one is that the spring constant is actually 5.2 times 10 to the 4 Newton’s per metre so you put that number here instead of 6.2 and the mass of the jumper is 75 kilograms so that goes there and there and with the fifth edition the answer is instead 36 centimetres.