VIDEO TRANSCRIPT

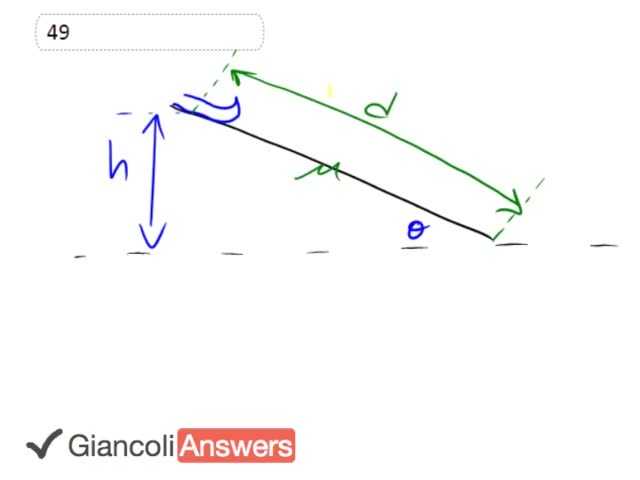
The ski is going to be sliding down the slope and the slope has a coefficient of friction mu. It’s going to travel at a distance ‘d’ along the slope and the slope is inclined at angle theta. And the question is given that there’s this friction involved what will be the speed of the ski at the bottom of the slope? It won’t have kinetic energy equal to ‘mgh’ because some of that energy will be dissipated by the friction. So the energy equation is that the initial potential energy – there’s no kinetic energy initially because it starts at rest is the final kinetic energy plus the work done by friction. So we’ll solve for the kinetic energy because that’s where the speed term is. Potential energy initial minus work done by friction. So that’s one half ‘mvf’ squared is ‘mgh’ minus the force of friction times, ‘d’ the length of the slope because that’s the distance over which friction is acting. And we’ll multiply everything by 2 over ‘m’ in order to isolate ‘vf’ here. So we have ‘vf’ – also taking the square root of both sides equals 2 ‘gh’ minus 2 times force of friction times ‘d’ over m. Alright. We have to do some work and dig into this friction force term. Now we know that friction is mu ‘fn’. So we need to know what ‘fn’ is. ‘fn’ is going to be the ‘y’ component of the gravity force. Let’s draw a picture up here and we’ll see why that’s true. We have here gravity with an ‘x’ component and a ‘y’ component. Here’s the ‘y’ component and then the ‘x’ component along the slope. It’s this ‘fgy’ that we’re interested in and there’s also a normal force sort of by the slope, perpendicular to the slope. This normal force has to equal the ‘y’ component of gravity because the ski is not accelerating vertically. Here’s our coordinate system; ‘x’ is along the slope and ‘y’ is perpendicular to the slope. So the normal force equals the ‘y’ component of gravity and theta is tucked in here which means that the ‘y’ component is the adjacent component of… adjacent leg of this triangle. So we’ll be using cosine to get that. So force of gravity is ‘mg’ and the ‘y’ component we get by multiplying that by cos theta. So that means friction force is mu ‘mg’ cos theta.

We also want to substitute for 'h'. We’re not actually given that number in this question. We’re given the 'd' the length along the slope instead. So we need to notice that ‘h’ is the opposite leg of this big triangle here. So since it’s the opposite leg we use sine to get that. So we multiply ‘d’ by sine theta to get ‘h’. So we’ll also notice that ‘h’ is ‘d’ sign theta. So we’ll make substitutions for both of those in our speed formula. So we get ‘vf’ equals square root of ‘2g’ times ‘d’ sine theta that’s what ‘h’ is minus 2 mu ‘mg’ cos theta times ‘d’ and that’s all divided by 'm'. So the substitutions were made in green. This is ‘h’ and this is force of friction. The ‘m’s’ cancel here. We can factor out the common factors 2, ‘g’ and ‘d’ from both of these terms and we get ‘vf’ equals square root of 2 ‘gd’ times sin theta minus mu cos theta. And now we’ll substitute in numbers. So we get 2 times 9.8 times 75 meter long slope times sine 22 degrees minus 0.09 times cos 22 degrees. And that equals 21meters per second is it’s final speed at the bottom of the slope. In the fifth addition this is 100m and it’s 20 degrees instead of 22 and the fifth addition answer is 22 meters per second.

For part B we have to ask given that speed at the bottom of the slope and assuming a level slope how far will it go horizontally along the assuming the ground is the same coefficient of friction? So now the ski is here and it’s zipping along sideways how far will it go? This distance ‘x’ is the question here. We know that its initial kinetic energy is going to equal the work done by friction. There is no final kinetic energy and there is no final potential energy so the only thing on the final side of this equation is just the friction term, the work done by friction. And initially there is kinetic energy and there’s no potential. So we have one half 'mv' initial squared equals the force of friction times ‘x’. We’ll solve for x. Divide both sides by force of friction. So ‘x’ is 'mvi' squared over the force of friction times 2. And we need to notice that the force of friction is mu ‘fn’ and ‘fn’ is equal to ‘mg’ because the ski is not accelerating vertically. So we have mu ‘mg’ for the friction force and we’ll substitute that in for ‘x’ or for into this ‘x’ equation. And the ‘m’s’ cancel giving us that ‘x’ is the initial speed squared divided by 2 mu 'g'. This initial speed… I mean it’s initial for this part B, but it was the final speed in part A. It’s the speed right here at the bottom of the hill. And we’ve calculated that already. It’s 21 meters per second. So we have ‘x’ equals 20.6883. That’s what it is to a whole bunch of decimal places. That’s what I rounded to 21 for the answer for part A. But these are the… these are all the decimal places before rounding divided by 2, 0.09 is the coefficient of friction and ‘g’. This is 2.4 times 10 to the 2 meters. So it’s going to go about 240 meters. For the fifth edition you have 22 meters per second here instead of 20.68. And the fifth edition answer is 290 meters.