VIDEO TRANSCRIPT

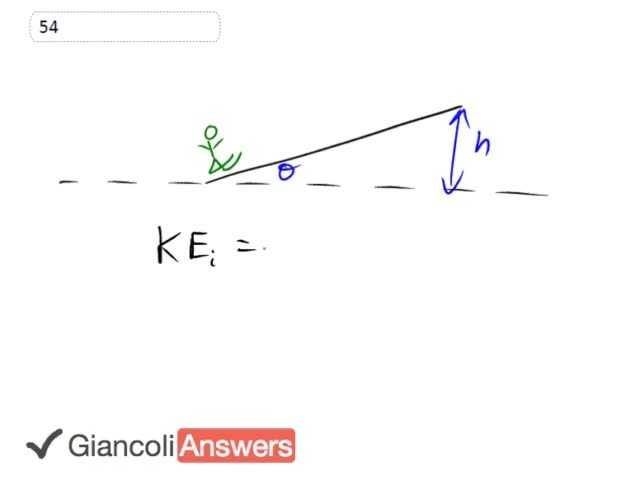
The skier has some initial kinetic energy at the bottom of the slope and they're going to glide up the slope which has friction to a point where they have some final potential energy. And the energy in this side of the equation is going to be final potential energy plus the work done by friction. There's no kinetic energy on this side because they come to a stop, okay. We'll do some substitutions into those expressions. So we have one half 'mvi' squared equals 'mgh' plus the force of friction times the distance along the slope.

So we have 'h' is the vertical height covered and this 'd' is the height along the slope, because friction is acting along the slope. So we want to just have to be apparel. Let's figure out what the friction force is and we'll make a substitution and then we'll find 'h' as well, substitute for that. And then eventually solve from u'. So the friction force is 'mfn' and we should draw a [free body] diagram to really explain how to get 'fn' here. I suppose that’s the skier, easier to draw him as a box here. Force of gravity straight down as a vertical component and a hold on to component along the slope. And there's also the normal force perpendicular to the slope and that’s what we're really interested in. That normal force will equal the 'y' component of gravity because there's no acceleration vertically.

Another coordinate system is 'x' along the slope, okay. It's not really that important but let's make it like that. So that means, while given that [fate] is tucked in there, the normal force is going to be the 'y' component of gravity and that’s gonna be the adjacent leg of this triangle, so we're going to use cosine to get that. So we have 'M' force of gravity times cos and that’s 'Mmg' times cos then. So that’s the friction force. The height is height 'h' the skier goes vertically upwards it's going to be d times sine theta. 'D' is the distance along the slope that he goes, so there is 'd'. And 'h' is the opposite leg of that triangle so you use sin, so we'll substitute for 'h' and for force of friction in this formula. So we have one half 'mvi' squared equals 'mgd' sine theta plus 'Mmg' cos theta times 'd'. So this was a substitution for 'h' and this was a substitution for the friction force. And we're using algebra here to solve for 'm'. First of all we get rid of all the 'm's because it’s a common factor with every term. Lets get the 'Mgd' cos theta on the left. We're going to take this over there and flip the two sides around, this is how it's going to work.

So we'll have 'vi' squared over two minus 'gd' sine theta and that will divide everything by 'gd' cos theta. So we're left only with 'M' on the left and on the right hand side we have 'vi' squared over two 'gd' cos theta and then the 'g' and 'd's cancel here for the second term and we're left with sin theta over cos theta. Sin theta over cos theta is actually ten theta. So 'M' equals 'vi' squared over two 'gd' cos theta minus ten theta, it's not really important to write the ten theta, but why not? So now we'll substitute the numbers and we'll have 12.0 meters per second and we'll square that divided by two times 9.8 times the distance along the slope, times cosine of the angle minus the tangent of the angle and this gives 0.308 as the coefficient of friction.