VIDEO TRANSCRIPT

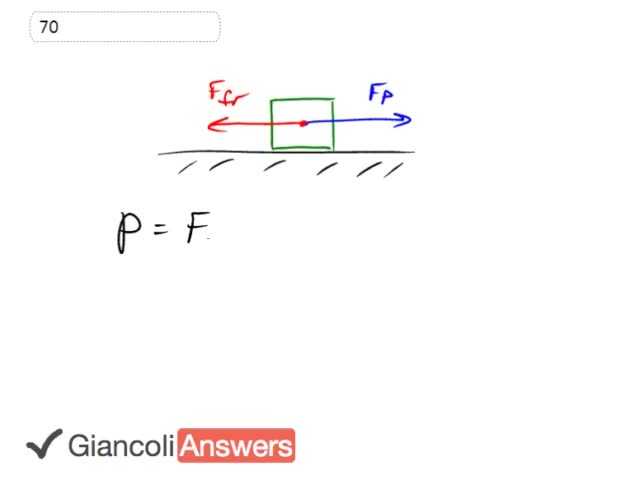
The power that this motor is going to need to drag this box along the floor is going to be equal to the force that it exerts times the speed that is dragging the box. The force 'FP' is going to be equal to the friction force because this box is going at constant speed so lets see if that's 'FP' equals force of friction and the force to friction is mue 'FN' and the normal force which I didn't bother drawing on there because it’s not accelerating vertically at all is going to be…'MG' because there is no acceleration vertically. So we have the pulling force is equal to friction mue 'MG' and we’ll make that substitution to the power formula, so if power equals…mue 'MG' times 'V' so we substituted [mue] 'MG' in place of the pulling force. S o the power necessary will be 0.45 coefficient of friction times 310 kilograms times 9.8 Newton's per kilogram times 1.2 metres per second, which equals 1.6 times 10 to the 3 watts and that asks for this in horsepower so we'll change that, 1.6 times 10 to the 3 watts times 1 horsepower for every 746 watts and this gives 2.2 horsepower is the required power of the motor.