VIDEO TRANSCRIPT

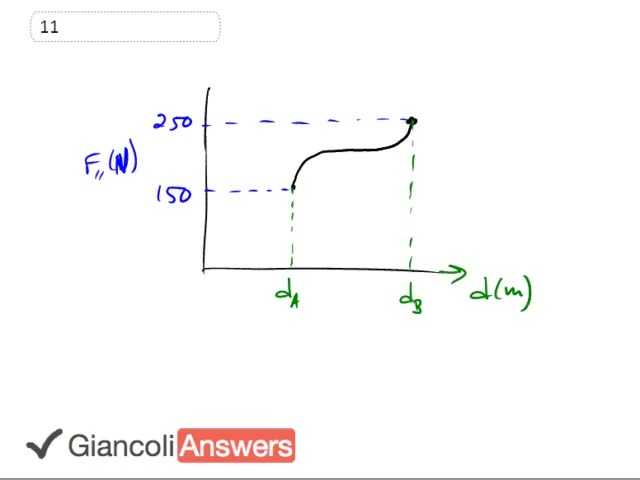
So I've reproduced my version of figure 6.6 a here and it seems to me that this point at the beginning lines up with 150 newtons on the 'y' axis. And this other far point lines up with 250 and so these points have coordinates 10.0 meters because we're told that 'dA' is 10. So 10, 150 newtons and then this point up here is coordinates 35.0 and 250 newtons. And well it seems to me that asking us to estimate it, and well if you wanted to do a super duper job I guess you would make a whole bunch of parallelograms in here and find the area of each parallelogram. But what we're going to do is, notice that we can draw a line between these two points. And we're underestimating the area in this region, because there's actually that little bit of portion we're missing there that I'm highlighting in blue. But we're overestimating for this region here and seems to me that the amount that we're over and underestimating should even out so that this is a relatively good approximation.

So we're going to consider this as one trapezoid and we're going to find the area of that. The trapezoid area formula, let me remind what that is. This is a trapezoid. And let's call this 'h1' height two and that base is here. And imagine that you took the same trapezoid rotated it and flipped it, and you'd end up with you can imagine that you could put it on top like this. This would be the base, this would be 'h2' and this would be 'h1'. So turn it over and then flip it upside down like that, you would be left with a rectangle, there is a rectangle there. That rectangle area is, well its one side times the other side, right? So its base times height. And the height in this case being 'h1' plus 'h2'. That’s the area of that full rectangle. The trapezoid is only half of that though. So the area for our trapezoid is going to be base divided by two times 'h1' plus 'h2'. That’s the formula we're going to use to calculate the area on this graph. 'h1' is 150, 'h2' is 250 and the base is 35 minus 10. So let's do that, the work done is going to be the area under the curve there, the area of the trapezoid. Base times 'h1' plus 'h2' over two, which is 35 meters minus 10 meters times 115 newtons plus 250 newtons divided by two. Then we end up with an answer of SOLUTION joules.