VIDEO TRANSCRIPT

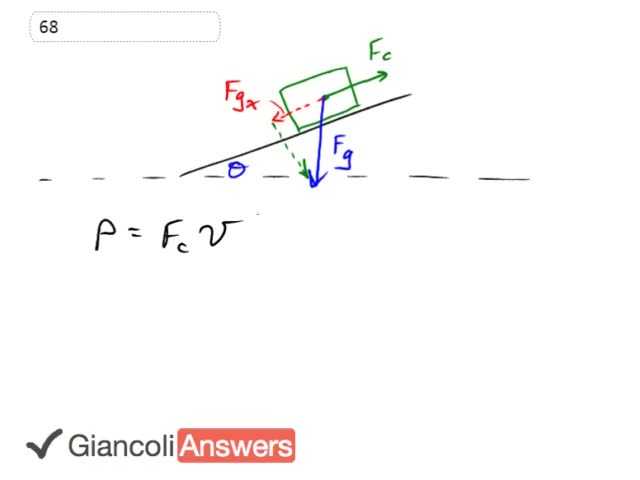
The power output of the cyclist is going to be equal to the force that they exert times their speed and they're going to be exerting a force in order to go a constant speed in re-exerting this force at ‘f’ subscripts ‘c’ the cyclist which will be equal to the 'X' component of gravity. The component of gravity that's going along the slope they’re working against some of our coordinate system is like this, okay. The angle theta is tucked in here so we can say that the…the force exerted by the cyclist is going to be the 'X' component of gravity and that is the gravity force is 'MG' times sine theta because this is the opposite leg of that triangle. Plugging that in for 'FC' in our power formula it gives us the power is 'MG' sine theta times 'V' then we can solve for 'V' we’ll divide both sides by this 'MG' sine theta. So 'V' equals power divided by 'MG' sine theta which is 0.25 horsepower which will convert into watts 746 watts per horsepower so these horsepower's cancel, and divide all that by 68 kilograms times 9.8 metres per seconds squared times sine of 6 degrees is the angle of inclination on the hill and the speed is 2.7 metres per second for the sixth edition and the fifth edition you have 70 kilograms here instead of 68 and the fifth edition answer is 2.6 metres per second and this value is reasonable because this works out to if you multiply that by 3.6 you get 9.6 kilometres per hour which is certainly doable for a cyclist.