VIDEO TRANSCRIPT

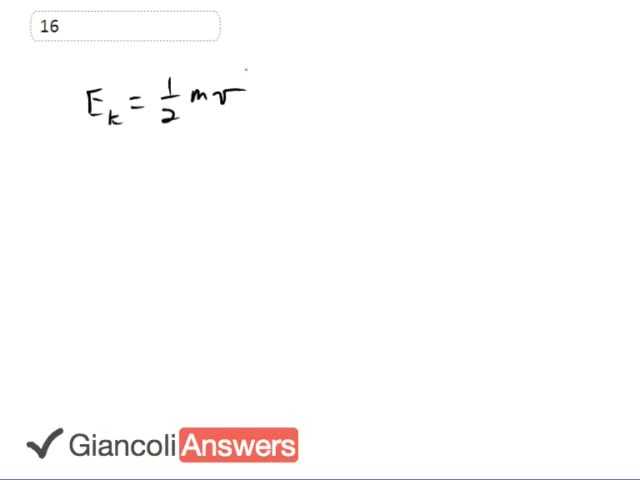
Knowing that kinetic energy is one half 'mv' squared we can solve for 'v' and then talk about how it changes with changes in kinetic energy. So we'll multiply both sides by two and divide by 'm' and then solve for 'v' square rooting both sides as well. We get 'v' is the square root of 2 times the kinetic energy divided by 'm'. So for part A of this question we're told that if kinetic energy increases by two times by what factor does the speed increase? We could say that in the one hand 'v1' would be 2 times 'kinetic energy 1' divided by 'm' and on the other hand for the second case when the kinetic energy is two times what it was before we'll have speed two will be two times well the kinetic energy in the second case divided by 'm' that's straight for the formula but we'll substitute for that 'ek2' and we'll say that it's actually 2 times energy of kinetic energy in the case one. So we can rearrange that slightly and show that this is the square root of two times '2e' 'kinetic energy 1' divided by 'm'. I'm writing it that way just to really make it clear that this is the same as this. And breaking this radical into two parts we can say it's root 2 times the square root of 2 'ek1' over 'm'. Okay so now definitely this is the same as that so this is 'v1'

So we can say that 'v2' equals root 2 times 'v1'. So our answer to this question is when the kinetic energy is doubled the speed increases by a factor of root 2. So the speed does not quite double it's about 1.4 times what it was before. For part B we have kinetic energy in the first case is one half 'mv1' squared in the second case we'll say it's one half 'mv2' squared by 'v2' is 2 times 'v1' so let's make that substitution one half 'm' times 2 'v1' squared notice that this 2 'v1' it's in brackets so this 2 here is gonna get squared and turned into 4. So this becomes 4 times one half 'mv1' squared. Well this is the same as this it's kinetic energy in the first case. So we can see that kinetic energy after the speed is doubled is four times the kinetic energy originally.