VIDEO TRANSCRIPT

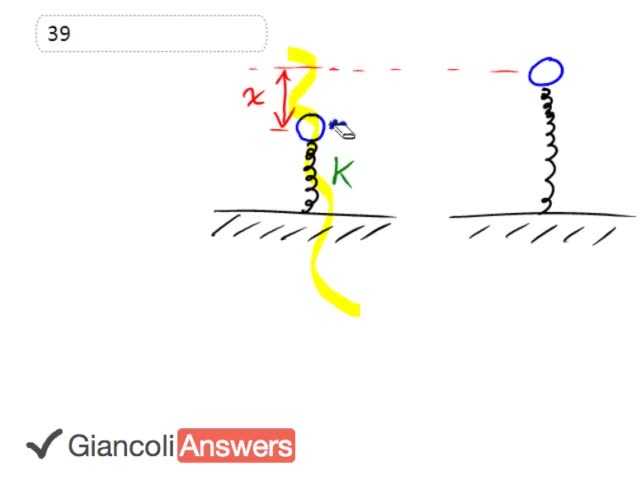
So in the first picture here we have the spring is compressed some distance ‘x’ and it has a ball of mass ‘m’ on it and the spring has spring constant ‘k’ when you let the ball go the spring is going to accelerate it upwards and then at this point where the spring is at it’s un stretched or uncompressed length that’s when the ball will have its maximum velocity because beyond this point the spring is going to be exerting a force the other direction on itself is going to be, it’s going to be decelerating itself, anyway this is where the ball gets released is when the spring is at its un stretched or uncompressed like…okay now we’re going to use the usual conservation of energy to answer this and kinetic energy initial plus potential energy initial is equal to kinetic energy final plus potential energy final. I’m not sure if I mentioned this is also the point where the ball has maximum speed because beyond this gravity is going to be slowing it down. Okay so that’s about that point right there it’s special ockie dokie and at the beginning here the initial kinetic energy is zero cause it’s not moving and we’ll say that the initial potential energy is one half ‘kx’ squared we’ll also say that this is our reference level for measuring gravitational potential in which case there is none. So the initial potential energy is all elastic potential given by one half ‘kx’ squared and that’s going to equal one half ‘mv’ final squared plus the gravitational potential it gains going from here up to here. So we have to solve for ‘vf’ we need to figure out this term so lets bring the ‘mgx’ to the left side by subtracting it from both sides we’ll flip both sides around as well and so we get one half ‘mvf’ squared equals one half ‘kx’ squared minus ‘mgx’ multiply everything by two and divide by ‘m’ as well and they end up cancelling the ‘m’ here and the 2 cancels with this half so we have ‘vf’ we’ll also take the square root of both sides as the square root of… ‘kx’ squared divided by ‘m’ there’s no one half on this term anywhere because we multiply by 2 minus ‘2gx’ so we’ll substitute in numbers we have the finals speed is 950 Newton’s per metre that’s in the sixth edition times 0.15 metres that’s squared divided by 0.3 kilograms minus 2 times 9.8 times 0.15 metres this equals 8.26 better stated as 8.3 metres per second. So that’s the speed of the ball at the top of its right there okay and part B.

We have the kinetic energy initial again is zero and the potential energy initial is all elastic and then the maximum height well the kinetic early kinetic energy is going to be zero there as well when it’s at the top of it’s path. So kinetic energy final zero kinetic energy initial is zero and the final kinetic energy or final potential energy will be entirely gravitational potential so this is the scenario where the ball is shot off sometime later in this picture the ball is going to be up here somewhere. So it’s going to have gone this distance flying through the air, okay but the real question is what is it’s height above it’s initial position? So this is what we’re actually going to answer is that height there. Well if we say that the initial potential energy is entirely elastic potential that means this must be the reference level for measuring height so given that that’s the case our final potential energy is going to be ‘mgh’ and we know that this ‘h’ is measured with respect to the compressed position not with respect to the top of the uncompressed spring because if there was any other reference level then there would have to be a potential energy term in the left side and, and since there isn’t that’s how we know that the reference point for measuring height is the compressed position. So we’ll solve for height divide by ‘mg’ and flip both sides around gives us that height is ‘kx’ squared divided by ‘2mg’ and that’s going to be 950 Newton’s per metre times 0.15 metres squared divided by 2 times 0.3 kilograms times 9.8 so the height above the compressed position is 3.6 metres now for the fifth edition changes, we have to change only this number here the spring constant is actually 900 Newton’s per metre in the fifth edition and that gives a launch speed which is a little bit less than it’s 8.03 metres per second, 3 [sick] figs in the fifth edition because it give the mass of the ball the 3 [sick] figs instead of two, again this gets changed to 900 Newton’s per metre and the fifth edition answer for the maximum height is 3.44 metres above the compressed position.