VIDEO TRANSCRIPT

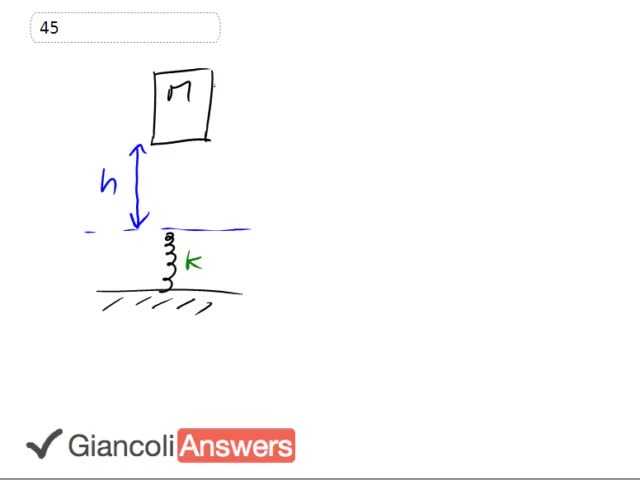
So the question here is what is the spring constant 'k'? Now what does that need to be in order so that the elevator when it falls from this height 'h' doesn’t experience an acceleration greater than 5 G’s? So we're gonna start by saying the energy initial kinetic and potential energy is equal to the final kinetic and potential energy that's how we start those questions in this chapter. And we'll say that the initial kinetic energy is 0 at the tope here where it starts to fall and then the final kinetic energy will also be 0 and that's when the elevator has fully compressed the spring. And this potential energy is gonna be 'm' and that's the elevator plus the occupants included 'mg' and its height. Now its height is gonna be 'h' plus however much it compresses the spring so let's call that 'x'. So the spring is gonna get compressed by a further 'x'. And if I were to make a little picture of sometime later you would have a compressed spring and an elevator on top. This is sometime later after the elevator falls and the spring ended up compressing this far that's 'x'. That initial gravitational potential that the elevator has is gonna equal ½ 'kx' squared the elastic potential of the spring when it's fully compressed. There's no gravitational potential in the final case because we've chosen the reference point to be this point of maximum compression and just so that there is no extra term there. We don’t want to have to talk about gravity on the right hand side there. Okay let's call that equation 1. And a different train of thought we're gonna now instead think about the forces that are on this elevator when it's on the spring. It's gonna have a force up on it, it's gonna have a force up equal to 'kx' that's the spring force. And it's also gonna have a force down due to gravity and the force up is actually gonna be significantly larger it's gonna accelerate upwards it's gonna rebound there. And algebraically we'll say 'kx' positive because it's up minus 'mg' negative or minus because it's down equals mass times acceleration that's the Newton's second law. And this has to be 5 Gs that's what the acceleration is.

So we'll say 5 'mg' we've substituted 5 'g' in place of 'a.' We're gonna solve this for 'x' and then substituting equation 1 with our result for 'x'. So we have that 'kx' equals 'mg' plus 5 'mg' where I've moved this term added it to both sides and then that becomes 6 'mg' and now we know that 'x' is 6 'mg' over 'k' alright so let's call that equation two. So we're gonna substitute for 'x' so we're gonna take this and put it here as well as here in equation one. I'm just gonna copy equation one 'mg' times 'h' plus 'x' equals ½ 'kx' squared okay. So we have 'mg' 'h' plus 6 'mg' over 'k' making a substitution there equals ½ 'k' times 6 'mg' over 'k' all squared. So let's multiply through by 'mg' so we have 'mgh' plus 6 'mg' squared over 'k' equals ½ 'k' times 36 that's what 6 squared is times 'mg' all squared over 'k'. Now I left this 'mg' all squared so that it's clear that this is a common factor among all these terms. So we'll divide everything by that, divide everything by 'mg' so this first term becomes 'h' and we have 6 'mg' over 'k' equals 18 'mg' over 'k'. This is a 'k' squared here actually. That squared [means] 'k' squared and one of them cancels with this one and so we're left with 'k' to the power of 1 in the bottom here. Let's multiply everything through by 'k' and also subtract both sides by that 6 'mg' and we'll be left with 'k' times 'h' equals 12 'mg' and dividing both sides by 'h' gives us this final result 'k' equals 12 'mg' divided by 'h'. And it's always nice to think about equations you got as answers and think about whether or not they're plausible or reasonable. And what this is saying is that as the height increases then 'k' should be decreasing does that make sense? Well if you imagine this elevator being higher up it would have a greater speed when it gets to this spring and so it would… you can imagine that it would require a greater distance over which to decelerate. And having 'k' smaller would allow that to happen. If 'k' was really big and the spring was rigid it would prevent the elevator from going very far as it's decelerating. So having a nice soft spring it would be more of a cushiony fall and that would, you require more of a nice soft cushion the higher up the elevator starts pulling.