VIDEO TRANSCRIPT

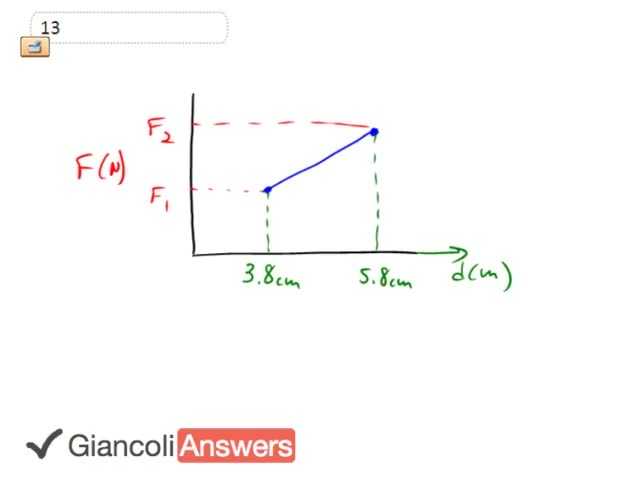
Here's a graph showing the force exerted on a spring in order to stretch it from 3.8 centimeters to 5.8 centimeters. And to figure out the amount of work needed to do that stretching, we'll have to find this area underneath the curve. So that’s the shape of the trapezoid and that area, is going to be we're going to find it using the trapezoid area formula which I derived a couple of videos ago. That’s going to be the base times height of one side plus the height of the other side divided by two and. Well, we need to figure out what these heights are.

So, knowing that a spring has a force, based on this formula the spring constant times the amount of stretching. We're told that the spring constant is 88 newtons per meter of stretching. So the force one in this graph is going to 88 times 0.038 meters, which is 3.344 newtons, and force two is going to be that spring constant times the other the final stretched length. Let's multiply there. So 88 newtons per meter times 0.058 meters, and that’s going to be 5.104 newtons. So those are the two heights of our trapezoid. 'f1' and 'f2'. The base is going to be the amount that has been stretched, the difference between 5.8 and 3.8. So it's been stretched 2 centimeters, which I'll have to convert into meters. So the work done is going to be that base which is 0.058 meters minus 0.038 meters.

At the end of this video I'll explain in more detail what that area of a trapezoid formula, in case you didn’t catch it in the last video. 5.104 newtons plus 3.344 newtons all divided by 2 and that equals SOLUTION joules or you could say SOLUTION millijoules if you felt like expressing it that way. Area of a trapezoid, we have this shape this side is 'h1' and this is h2' and then the base. And if you imagine flipping this trapezoid around and then putting it on top of itself, you can imagine stacking it on top of itself like this. This would be 'h1' and this would be 'h2' here with 'b' on the top. And this whole thing is a rectangle and the area of that rectangle is going to be length times width or base times the full height which is 'h1' plus 'h2', that’s the area of the rectangle. The area of the trapezoid you can see that the trapezoid is half of the rectangle, because the rectangle consists of two of these trapezoids. So the trapezoid area is half the area of this rectangle. So the area of the trapezoid is going to be one half of this formula we have above here. So that’s the area of the trapezoid and we use that to answer this question.