VIDEO TRANSCRIPT

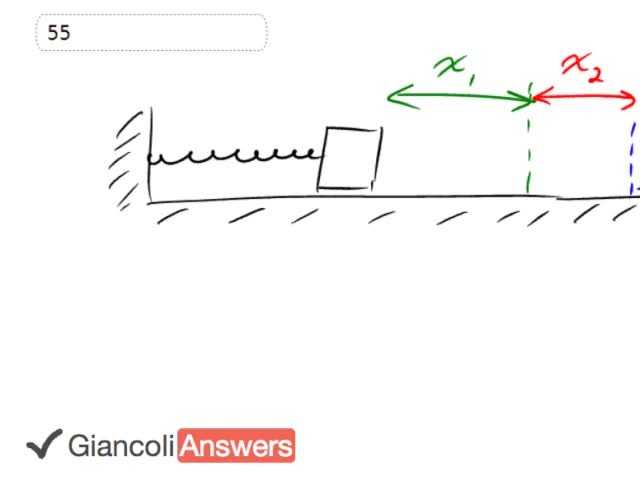
This block is compressed a distance 'x1' and then you let it go. And it goes out to this other position 'x2' stretched beyond the equilibrium position, and 'x2' is not as big as 'x1', so there's some energy lost due to friction. And our job is to figure out what is the coefficient of friction of this table. So we'll say that the potential energy that it has, in case one, which is drawn in black, equals the potential energy in position two, outlined in blue, plus the work done by friction. Work done by friction accounts for the initial energy that has been lost in the second position. So we have one half 'kx1'squared equals one half 'kx2' squared plus the friction force. The work done by friction is the friction force times the total distance over which it acts. Which is 'x1' plus 'x2'. Now the friction force is, 'mµ mg'. So I make that substitution, and also take this term more to the left side. We end up with one half 'kx1' squared minus a half 'kx2' squared. You close mµmg times 'x1' plus 'x2', then, we'll flip the two sides around, and simplify a bit.

Also divide by 'x1' plus 'x2'. So we get 'mµ mg' on the left after we flip the two sides around. Equals 'k'/2 times 'x1' squared minus 'x2' squared. So we factor the 'k' out from both of these terms. Divided by 'x1' plus 'x2'. You might recognize this as being the difference of squares, it should be anyway. There, that's the difference of squares and there's a pattern for factoring it. And let's do that. So we have mµmg times or equals 'k'/2 times 'x1' plus 'x2' times 'x1' minus 'x2'. That's the factored form for a difference of squares. And it turns out that these and these are a common factor in talking about them, so they cancel, which simplifies things a bit. And we'll also divide by 'mg' in both cases here. We end up with 'mµ' equals 'k' times 'x1' minus 'x2' divided by 2 'mg'. So now we can substitute the numbers, and get our answer. So we have 180 Newtons per meter as the spring constant, times 'x1' which is 5 centimeters, minus 'x2' which is 2.3 centimeters, I'm converting both of those to meters. And this is…'x2' is positive, we're just using magnitudes here because the potential energy of a spring, it doesn't matter whether it's stretched or compressed, it's the same either way. So we'll just use magnitudes. And we have .620 Kilograms, and 9.8 Newtons per Kilograms, and this gives us a coefficient of friction of .40. And for the 5th edition, you have a slightly different mass of .520 Kilograms; otherwise the numbers are the same. And so for the 5th edition the coefficient of friction is .48.