VIDEO TRANSCRIPT

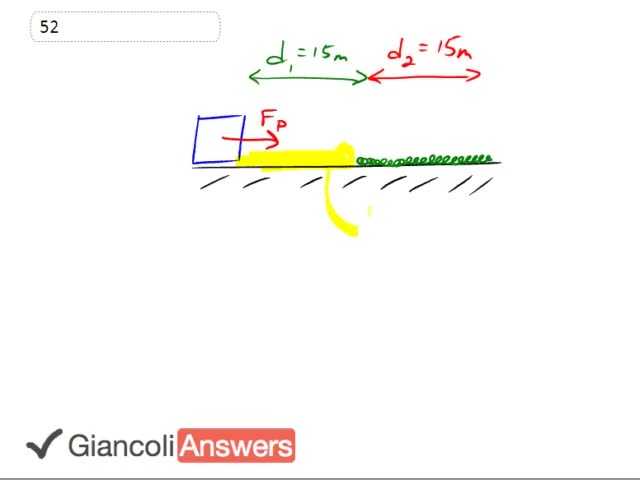
There's boxes being pulled along a surface that’s initially frictionless in this region in the region 'd1' and then the surface becomes a surface with friction over this region, so I've drawn it with rough squiggly green stuff there. So the question is what will its final speed be? So there's only the pulling force in this first region, and the second region there's both the pulling force accelerating it forwards and the friction compensating a bit going backwards. Or we're going to solve this using energy, so we'll say the change on kinetic energy is the network and the network is going to be the network done in stage one.

That’s the stage here where there is no friction plus the network done in stage two, that’s where there is friction. The network done in stage one is just the net force times distance, but there is only one force, that’s the pulling force. So it’s the pulling force times 'd1'. The network in the second part is going to be the net force in that second region times 'd2' and that net force will be the pulling force minus the friction force times 'd2' and that is a pulling force minus 'Mmg', that’s what the friction is 'mfn' and the normal force is equal to gravity because its not accelerating vertically, okay. So that means the network is pulling force times 'd1' plus pulling force minus 'Mmg' times 'd2'. That’s the network and that’s the change in the kinetic energy. So one half 'mvf' squared, there is no initial kinetic energy because it starts at rest. So its change in kinetic energy is just going to be this one term. That is going to be equal everything we have here. 'Fpd1' plus 'fp' minus 'Mmg' 'd2' and we'll solve for 'v'. We'll multiply everything by two over 'm' and then take the square roots to both sides. So you get 'vf' is square root of two over 'm' times 'fpd1' plus 'fp' minus 'Mmg' 'd2'.

So we have a final speed looking at numbers now of two divided by 110 kilograms times 350 Newtons pulling force times 15 meters for that 1st region plus 350 Newtons minus .3 coefficient of friction times 110 kilograms times 9.8 times d2 that 2nd region length which is also 15 meters all that gets square rooted. And the answer is 10 meters per second for the sixth edition. For the fifth edition a minor change is to put 90 kilograms instead of 110, everything else is the same. The fifth edition answer is 12 meters per second.