VIDEO TRANSCRIPT

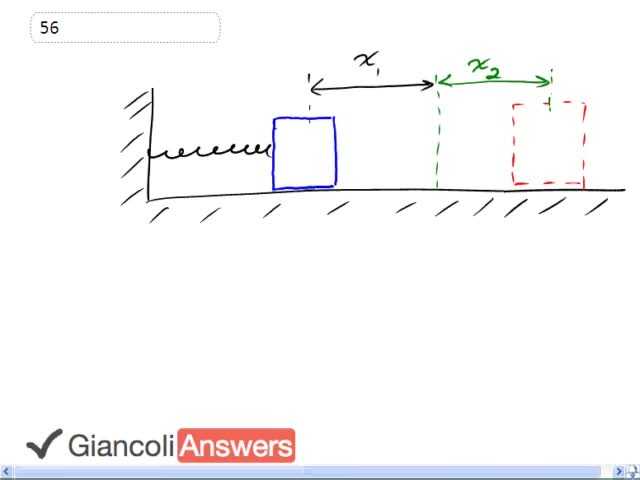
If you like a challenge then this is a good question for you. Let's set it up first a little bit explain what's going on we have a force that's pushing this block back and compressing the spring we'll call that the applied force and the spring must be pushing back with the same force since it is stationery, there is no net force so this is the spring force. And if you let this block go, it will spring back to this position some distance 'x2' beyond the equilibrium position where it will be you know before it was compressed.

So the question is what is this 'x2'?

And there is a variety of things we need to figure out before we can answer that.

Number one we need to know what the spring constant is then we can, we can say that the spring force that’s pushing back here that's the one in green here equals the applied force and the spring force we know is given by the formula k spring constant times the amount of the compression 'x' we'll call it 'x1' and then solving for 'K' because 'K' is the applied force divided by 'x1' and we know both of this things we know the applied force and we know 'X1' so we have to figure out 'K'. We'll say that the potential energy in position one that's going to equal the elastic potential. And there is no Kinetic energy in position 1 because it's stationary there. So this elastic potential we're going to substitute for 'K' from this expression. So we have one half times 'fa' over x maybe you'll like the different colors for substitution 'Fa' over x times, that's 'x1' times 'x1' squared and this works out to one half 'Fa' times 'X1' the, this 'x1' cancels with one of the 'X1' there this is our potential energy in position 1

That’s one half the applied force times 'x1', now the conservation of energy idea is that the potential energy in position 1 is going to equal the potential energy in position 2 plus the work done by friction from this point to this point. So not all of the potential energy in position 1 makes it to the potential energy in position 2, because of this energy dissipated by friction en route. So the position one potential equals position 2 potential plus the work done by friction. We'll make substitutions for each of these terms potential energy in position 1 we have already figured out as one half 'Fax1' and in position 2 we have one half 'Kx22' and I bet you can guess that were going to substitute for K in a second and plus the work done by friction which is the friction force times the total distance that it's acting over so that’s 'x1' plus 'x2'.

And the question, is what is 'x2' so we're going to be doing a whole bunch of algebra to solve for that. Lets first as ourselves, what is the friction force because we know what mu is and we know the way to the block and so based on that we'll figure out friction force. So with mu 'fn' is the regular formula mu 'mg' in this case because there is no vertical acceleration so the normal force equals the weight. Also keeping in mind that K is 'Fa' over 'X1' just reminding you of that from, from above just copying that from here, we're going to make those two substitutions into this formula we're going to substitute for friction force and we're going to substitute for K in this next line.
.
So we have one half 'Fax1' equals 'Fax2' squared over '2x1' because, maybe different colors would be better there? That 'k' is 'Fa' over 'x1' and then we have the 'x2' squared to begin with and then there is the one half plus the friction force umg times 'x1' plus 'x2'. Okay off to the races with algebra. This is a quadratic formula for x2 and so were going to have to set it up, everything on one side equals to zero and use quadratic equations. So have one half Fax 1 equals were just going to expand the bracket here and then will make collect terms together. let's bring this over to the right hand side and flip the two sides around and we'll say equals zero so we have Fax22 over 2x1 plus mumgx2 plus mumgx1 minus Fax1 over 2 equals zero. There is a quadratic equation this is going to be A this is going to be b and this whole thing is going to be C and what I'm talking about there is when you have a quadratic equation of the form ax2 +bx+c you use the formula x equals negative b plus or minus square root b squared minus 4 ac over 2a.

I'll tell you what each of these a b and c are and then we'll leave it up to you to substitute it into the quadratic formula. So we have Fa is 22 Newton’s in the sixth edition, x2 squared over 2 times point 1.8 meters plus point 3.0 is the co efficient of friction, mass of the block is point 2.80 kilogram’s in the sixth edition times 9.8. That’s times x2 plus mu again point 3 times point 2.80 kilogram’s times 9.8 times point 8, point 1.8 meters that’s 18 centimeters the amount that it was compressed that's x1., minus 22 Newton’s times point 18 meters again divided by 2 all that equals zero.

Holy smokes that’s a long expression. If you calculate this coefficient of x square that works out to 61.111 x2 squared then we have +0.8232x2 minus 1.8318 equals zero. So this whole, this whole thing here works out to 1.8318. And plugging into the quadratic formula you get, 2 answers as usual and we're going to take the positive one so X2 is 0.17 meters which is 17 centimeters and the reason we take the positive one is because of the way the formula was set up originally. We, we said that the total distance over which friction is acting is X1 plus X2 and that’s because, so that means by saying that we've implicitly defined this X1 and X2 as magnitudes so they're not absolute positions on a coordinate access instead they're distances so, versus displacements so this are distances so that’s why its going to be positive.

Another reason is to say that your other answer is point 18 and that point 18 we expect as an answer because that is the, the largest displacement on this side of the block. It starts at point 81 meters so that’s the physical interpretation of that other, sort of mathematical artifact it just comes because of the math but the physical reason for that, is it's just telling us there is a maximum extension of 18 centimeters as well, well we already knew that because that's where it starts.

Okay lets talk about the fifth edition for a little second here, the fifth edition it's actually the same answer as 17 centimeters but you get it at slightly different ways so this is 20 Newton’s there, point 18 kilogram’s 180 grammes. And then you change the mass here again and 20 Newton’s. So it's interesting how all this you know changing from point 28 to point 18 is a large, change but the answer becomes the same because of a different force and the coefficients that you'll get for the fifth edition is fifty five point five six X2 squared plus point five two nine two times X2 minus one point seven zero four seven equals zero so that's your quadratic equation that you to solve and you get the same answer 17 centimeters