VIDEO TRANSCRIPT

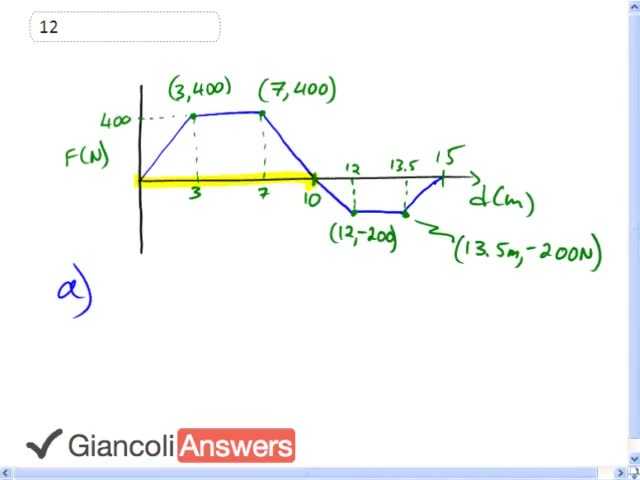
So here's the figure in the text book. For part A we're finding the work done between zero and ten seconds, and we'll find that by calculating this area 'A1' plus 'A2' plus 'A3'. We could use a trapezoid formula for this one, but maybe it’s a little more obvious why it's this triangle 'A1' plus this triangle 'A2' plus this triangle 'A3'. We can calculate it anyway we like. So we have the work done is 'A1' plus 'A2' plus 'A3'. Area of a triangle is one half base times height, and the way I see it, this point lines up with 3 meters and 400 newtons. We have another point lining up at seven meters and 400 newtons and the whole thing ends at ten seconds. So 'A1' is one half times the base being 3 meters times the height of 400 newtons, plus area two is 4 meters. That’s the difference between seven and three, times the height of 400 newtons. Then 'A3' is one half times three meters again, that’s the difference between 10 and 7. Times the height of 400 newtons, this gives an answer for part A of 2,800 joules of work done between zero and ten seconds.

In part B we calculate the work done for the entire time from zero to 15 seconds. And we can see that there is some negative work being done here because the force is going against the direction of motion. So that’s going to reduce the total work done, so we'll be subtracting those areas. So we'll call that area four, area five and area six. So the work done in part B is going to be 'A1' plus 'A2' plus 'A3' minus 'A4' minus 'A5' and 'A6'. So 'a1' 2 and 3 we already know is 2,800 so let's just write that down. And then we're going to subtract away between 10 and 12 that’s two seconds, so that’s the base, is two. And we'll multiply that by a height of 200. I've already got the negative sign accounted for here, so we don’t need to go negative 200.

So we have two times 200 newtons, that’s 2 meters times 200 newtons divided by 2 minus 1.5 meters times 200 newtons, that’s the little rectangle. That’s this 'A5', that’s 1.5 times 200 newtons. And then we'll also subtract away the last triangle there, 'A6'. So we have one and a half meters times 200 newtons divided by two. And the answer here, total work done from zero to fifteen seconds is approximately 2,150 joules.