VIDEO TRANSCRIPT

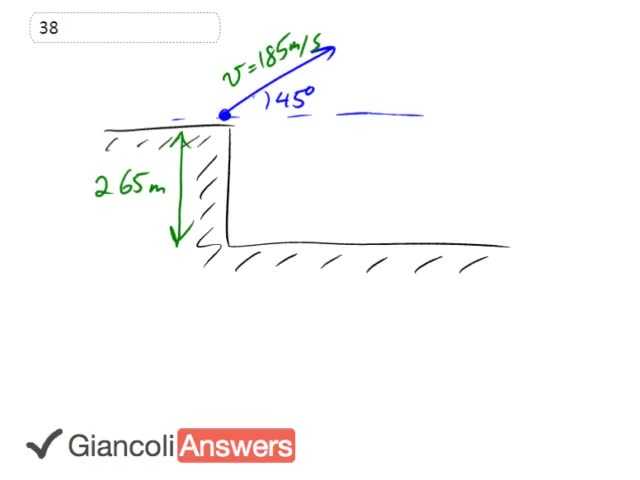
So this projectile is fired with a speed of 185 metres per second at an angle of 45 degrees to the horizontal from the top of a cliff that’s 265 metres up. Now we’ve answered questions like this, the question being what’s going to be the speed once the ball gets down to this point what’s going to be the speed here and we’ve answered questions like that in the past and it involved taking the vertical component of the velocity and applying the acceleration due to gravity is taking into account there vertically speaking and then horizontally speaking the horizontal velocity is constant and so on and so on. And we’re going to do this question now instead with conservation energy and I think you’ll see that it’s a lot simpler because it’s energy is not a vector and that’s one of the main reasons why it’s useful because it’s not a vector we don’t need to deal with directions. So we have kinetic energy final plus potential energy sorry, kinetic energy initial plus potential energy initial is the final kinetic energy and potential energy. That is to say that one half ‘mvi’ squared plus ‘mgh’ equals one half ‘mvf’ squared plus zero; there is no potential energy in the end because we’re going to choose the ground to be our reference level. We’ll solve for ‘vf’ so we’ll divide everything by ‘m’ so the ‘m’ cancels and multiply everything by 2 and take the square root of both sides and put ‘vf’ on the left cause that’s where you want to have your unknown so ‘vf’ is the square root of ‘2gh’ plus ‘vi’ squared. Substituting in numbers we have 2 times 9.8 times 265 metres plus 185 metres per second and we square that, and this gives 199 metres per second.