VIDEO TRANSCRIPT

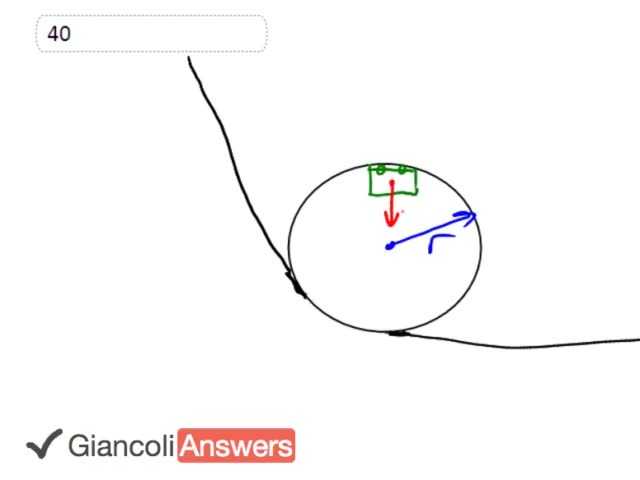
When this block is at the top of the loop the loop, the free body diagram will have only gravity on it for the minimum speed it was going faster than the speed then you’d also have a centripetal force provided by the normal force as well it was going really fast. But we want the minimum speed necessary because we’re looking for the minimum height that it has to go above this loop and or above the ground level here in order to make the loop. So we’re going to have centripetal force be provided entirely by gravity. So at the top of the loop at the top of the loop we’re going to say the following things, we’re going to say the kinetic energy is going to be one half ‘mv’ squared and that’s going to equal well we’d better we better say something about these forces here so at the top of the loop again we’re going to say that the normal force plus the gravity equals ‘mv’ squared over ‘r’ and I mention that the normal force is zero so this is a way that we can solve for the speed ‘v’ so multiply both sides by ‘r’ and we get that ‘mv’ squared is ‘rfg’ but ‘fg’ is ‘mg’ and we can cancel the ‘m’ from both sides giving us the ‘v’ squared is ‘rg’ I’m going to leave it at that there’s no need to take this square to both sides, so we’ll substitute that result up here and so we can say that the kinetic energy at the top of the loop is one half ‘mrg’ where ‘rg’ is ‘v’ squared according to this, now the potential energy at the top of the loop is equal to ‘mg’ times 2 times the radius this height here because we’re going to measure with respect to this ground level this height is 2 times the radius of the circle. And then we’ll say the usual stuff that the kinetic energy and potential initially add up to the final kinetic and potential, so lets talk about…at initial position…here’s the initial position right here so now we’re talking about this position there. That position we can say that kinetic energy is zero cause it’s not moving and the potential energy initially is ‘mgh’ where ‘h’ is the height above this level here and that’s the whole question is to figure out what ‘h’ is. So knowing that the total initial energy is equal to the total final energy we’ll say that ‘mgh’ equals one half ‘mrg’ where we’re substituting from here, substituting for kinetic energy and the potential energy there is ‘mg’ times ‘2r’ we’ll divide everything by ‘mg’ and that will solve for ‘h’ so we have ‘h’ equals a half ‘r’ plus ‘2r’ which ‘2.5r’ so height has to be 2 and a half times the radius of the circle in order for the cart to go around it without falling off the top.