VIDEO TRANSCRIPT

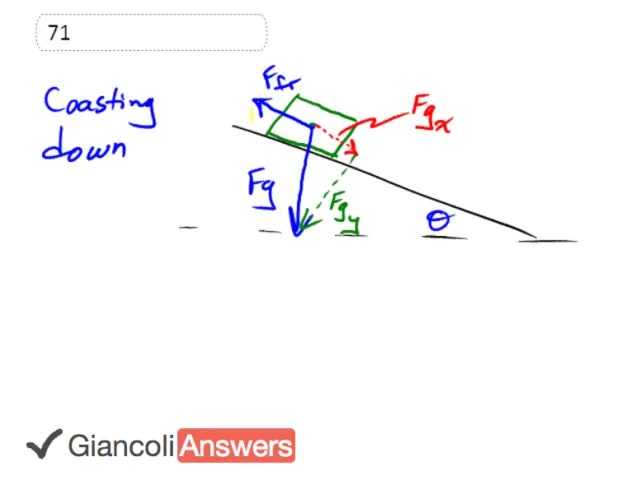
We know that when the cyclist is coasting down the hill, since it's going at a steady speed, the friction force that they're experiencing must be equal to the component of gravity that's pulling them down the hill. And when the question gives us this information about them coasting down the hill the whole purpose of that is so that we can figure out what his friction force is and then we'll use that answer in the next part of the question where we talk about them climbing up the hill.

So what is that friction force?

It is the 'x 'component of gravity and being the opposite component of this right triangle, this opposite leg of that right triangle the gravity force triangle means where you sign when you get it. So that’s Mg is the force of gravity times sin theta that’s gonna be the friction force now lets talk about when he's climbing up we'll need a new picture for that.

He's going to be exerting some force to get himself up the hill so we'll call that the force of the cyclist. And there will be gravity straight down which has components working against him here. That’s the 'X' component of gravity pulling him back. There's a y component as well though that's not important. And there is also friction holding him back. How much friction? This much, that’s what we figured out up here and we know the friction is going to be the same because the speed's the same. Air friction just depends on the speed. It depends on a lot of things but everything is the same in these two scenarios. So that's the force of friction.

So we know that the power out put is going to be the force that he exerts, the cyclist times his speed and we also know from Newton's second law whether the fact there is no un balanced forces, we know that the cyclists force is going to equal the 'x' component of gravity plus friction. The 'x' component of gravity again this is the opposite leg. So we use sin theta to get that so we have 'MG' sin theta and then we'll substitute for the friction force which we found up here. Turns out it's actually the same as the 'x' component of gravity plus 'MG' sin theta again. So the force of the cyclist is '2mg' sin theta. So we'll substitute that into our power formula so that's '2Mg'sin theta times the speed so we substituted this in place of that and the power out put is going to be 2 times 75 kilogrammes times 9.8 newtons per kilogrammes times sin 7 degrees times 5 meters per second, and we get 895.7 watts. Let's write that with 2 'sig figs'. 9.0 times 10 to the two watts is the power required for the cyclist to climb the hill at 5 meters per second.