VIDEO TRANSCRIPT

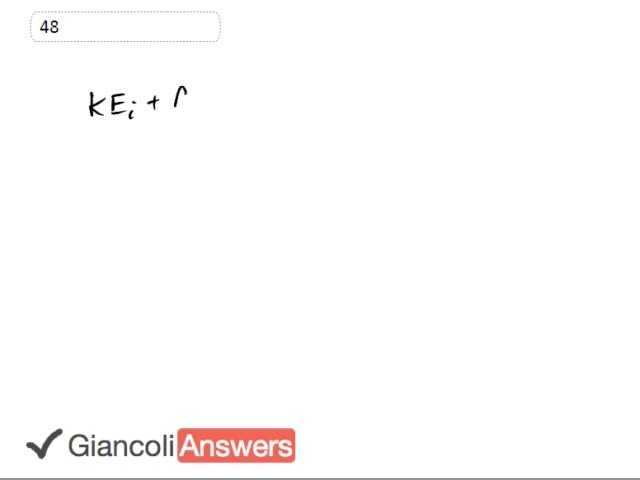
The total initial energy equals the total final energy. And initially we have kinetic and potential and in the end we have kinetic, potential and this extra work done by friction. So this is all the energy we started with and some of it went into friction and whatever is left over became the final kinetic and potential. So we're going to figure out that work done by friction is. The child starts at rest at the top of the slide, so this is zero. And at the bottom of the slide there's no gravitational potential because the bottom of the slide is our reference level that we're measuring potential energy with respect to.

We solve for the work done by friction and its 'mghi', that’s the initial potential minus the final kinetic energy. One half 'mvf' squared. So this [board] equals zero if there is no friction. This difference here will be zero if there's no friction. But since there is friction, there's going to be some energy which doesn’t appear as kinetic. So some of the potential energy that it starts with, some of it turned into kinetic but some of it also turned into thermal energy which is what we're finding right here. That’s 'm' times 'ghi' minus 'vf' squared over two. So we'll substitute in 21.7 kilograms times 9.8 times 3.5 meters minus 2.2 meters per second, that’s the speed of the child at the bottom of the slide squared divided two. This is 6.9 times 10 to the two joules.

In the fifth edition, you make some changes to these numbers. Its 17 kilograms instead of 21.7 and the speed at the bottom of the slide is two and a half meters per second, also squared. So for the fifth edition, the work done by friction is 5.3 times 10 to the two joules.