VIDEO TRANSCRIPT

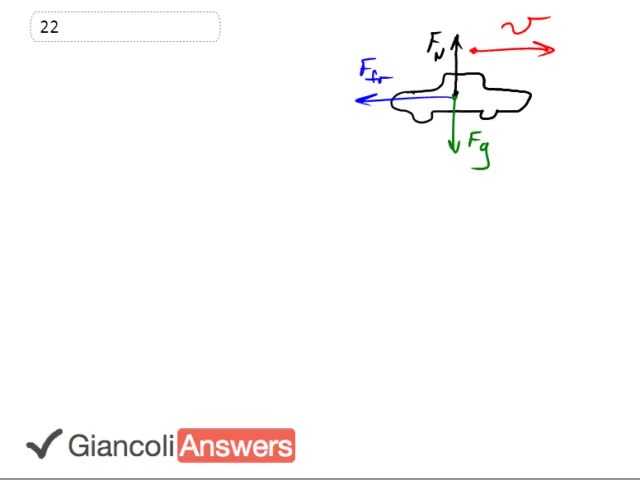
So we have a drawing of this car showing all the forces acting on it. Friction is what’s going to be stopping it and we have the gravity pointing straight down and the normal force of equal magnitude pointing up. We know it’s equal magnitude because it’s not accelerating vertically and we need to know that normal force in order to calculate friction because friction is ‘’ the coefficient of friction times the normal force. Since the normal force is the same as gravity we have that the friction force is ‘mg’. But that’s getting ahead of things a little bit. What we want to say then is that the change in kinetic energy is the net force times ‘d’, the net force in this case being friction. So we’re going to substitute this here in a minute. We can also say that the change in kinetic energy is one half ‘mvF’ squared minus one half ‘mv’ initial squared, but the final speed being zero. We’re just going to deal with magnitudes here, too. So we’ll take the size of the change in kinetic energy is going to be one half ‘mvi’ squared. Basically what I’m saying is ignore the negative sign here ‘cause we’re just going to deal with the size of things. And we’ll say that one half ‘mvi’ squared equals ‘mgd’. This ‘mgd’ is the work done by friction where the friction force is ‘mg’ and the work done by that friction force is multiply that force by ‘d’ where d is the length of the skid mark. So we can solve for ‘vi’ here. So multiply both sides by two and divide by ‘m’; so times by two and divide by ‘m’ taking the square root of both sides as well gives us the initial speed must have been square root of two ‘mgd’. Notice that the ‘m’s’ cancel then both sides. Yeah. Alright. So we have square root two ‘mgd’. So the initial speed is square root of two times .42 times 9.8 Newton’s per kilogram times 88 meters. This gives us an initial speed of ANSWER meters per second.