VIDEO TRANSCRIPT

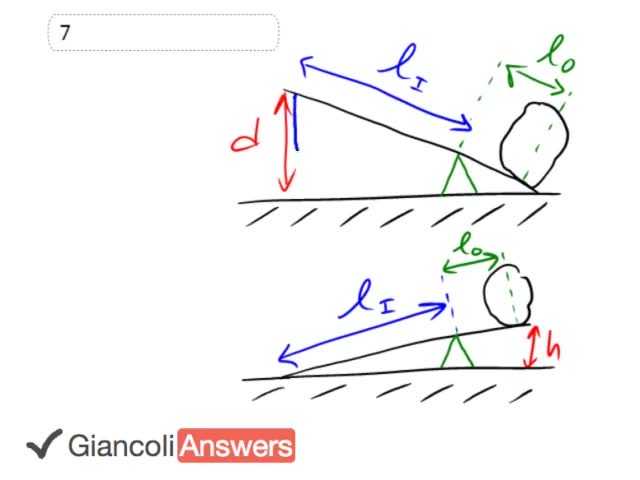
What we're going to show here is that the work done by the man exerting a force straight down here. We assume it's straight down, otherwise this question would be really difficult to answer, so it's straight down along this distance 'd', that's the force input. The work done by that force, which is going to be work input equals the force input times the distance that it goes over, 'd' here. That work equals the work output, that's what we're...we're starting with that assumption. And the work output is the force out exerted on this rock, 'f' out which exerts over this distance 'h'. That's the distance over which the output force acts. And so the work done by the output force, work out is the force out times 'h'. And the amount of work done in each case is the same. So we can say, that 'Fid' equals 'Foh.' Well that doesn't quite answer our question, because we have to show that 'F' out divided by 'F' in, equals the length of the lever arm in, divided by the length of the lever arm out. And this formula says nothing about lever arms, and so that's where going to be, where our work is going to be involved. Is showing how 'd' and 'h' are related to the lever arms. The lever arm for the input force and the lever arm for the output force. We're going to use similar triangles to show this, that they're related. Now let's consider 'd' first and think about this pivot point, which has some height we call 'p' for pivot, and consider the triangles here, this big triangle and this smaller triangle involving the pivot. Those two triangles have all the same angles, because they share this angle theta here, and they each have 90 degree angles. So if two angles are the same, the third must be the same as well. So these angles or these triangles have all same angles, which means the triangles are similar. And similar triangles have equal ratios of their corresponding sides. So if we take side 'd' and divide it by the hypotenuse of that big triangle, then that will equal side 'p', which is also opposite theta, divided by the hypotenuse of the small triangle. And then we'll be able to relate 'd' to the lever arms. And then we'll do the same kind of story for the second picture down here involving 'h'. And then one thing leads to another and you see how this gets us the answer. So find d in terms of the lever arms. So we know that 'd' divided by the hypotenuse of the big triangle, which is the input lever arm plus the output lever arm, that hypotenuse is the sum of those lever arm lengths. That's going to equal 'p' divided by the output lever arm. Okay, and then we'll solve for 'd'. So 'd' equals 'p' times 'li' plus 'lo' divided by 'lo', okay. And then we'll find h. The reason we know that we have to do this is because, we know that 'd' and 'h' need to be related to the lever arm, somehow. So this is what we're thinking, is good way to relate them. And so we have this height of the pivot is 'p' here again, and we're going to say that h divided by this full length, which is 'lo' plus 'li', is going to equal 'p' divided by 'li '. So we have 'h' divided by 'lo' plus 'li', equals 'p' divided by 'li'. And solving for 'h', gives us 'p' times 'lo' plus 'li', divided by 'li'. Now we're going to make substitutions into this formula here for 'd' and 'h', so we're going to plug 'd' into there, this expression. Then we'll also plug in, this expression for 'h' in that formula. Let's rewrite the formula here so we can see it a little better. We have force input times 'd' equals force output times 'h', okay. The substitutions look like this, the force input times 'p' times 'li' plus 'lo', divided by 'lo' equals force output times 'p' times 'lo' plus 'li' divided by 'li'. So this ended up going here because that's what 'h' is. We can see that there is some common factors on both sides 'p' is a common factor, so it cancels. 'li' plus 'lo' is also a common factor and what we really have here is 'fi' divided by 'lo' equals 'fo' divided by 'li'. We do some algebra rearrangement, and this becomes 'fo' divided by 'fi', equals 'li' divided by 'lo' which is what we had to show.