VIDEO TRANSCRIPT

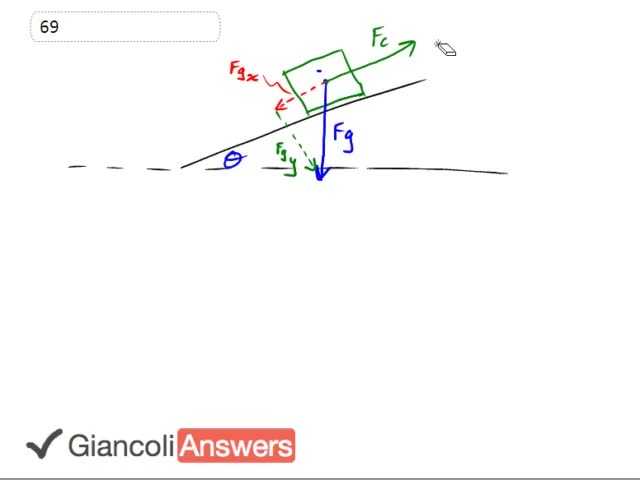
When this car is climbing the hill it's gonna be exerting some force in order to compensate for the 'x' component of gravity or the component of gravity along the hill pulling it backwards and also compensating for the force of friction. Let's draw that in a different color, the gravity one. So we have the force of friction pulling it back as well. Now since it's going at steady speed this friction force and the 'x' component of gravity must be the same as the car's driving force. So we're Going to say that, the friction force or so the other force exerted by the car equals the 'x' component of gravity notice that theta's tucked in here by the way. So we're gonna be using sin in order to get that component, plus the friction force and the reason this is important is because we know that the power output of the car is going to be whatever force it exerts times it's speed. So we're looking for this 'FC' force exerted by the car. Continuing this work here we have force exerted by the car is 'Mg' sin Theta force of gravity times sin theta cause it's the opposite leg. And plus the friction force which we were given in the question. Substituting that into our power equation.

We have power is 'Mg' sin theta plus the friction force times the speed. So we substituted this in place of the car force. And we have to solve for Theta here to find the maximum angle of inclination that this hill could have. So we'll expand this bracket here and multiply through by 'V' and then subtract this from both sides and flip the two sides around we get 'VMG' sin theta equals the power out put minus 'V' times the force of friction and we'll divide both sides by 'VMG'. Giving us that sin theta is power minus 'V' times force of friction divided by 'VMG'. And so theta is going to be the inverse sign of all that so I'll plug in numbers here. We have a hundred and twenty horse powers which will have to change into Watts .764 watts per horse power. This horse powers will cancel giving us watts which is good we need meters kilogrammes seconds type units here 'Mks' units and minus 650 newtons.

Times the speed of 75 kilometers per hour which will change to meters per second by dividing by three point six all that is divided by, that’s 'b' converted again, times 1,200 kilogram’s times 9.8 newtons per kilogrammes these are the sixth edition numbers we'll get to the fifth edition in a second. This works out to 18 degrees as the maximum angle he hill can have in order for the car to climb it at that speed it will have to go slower than 75 if the hill was any steeper. For the fifth edition the friction force adds up to 600 newtons instead of 650 and the cruising speed of the car is only 70 kilometers per hour so you can imagine that it's able to climb a steeper hill, the car is also lighter another good reason why it can climb a steeper hill and you pluck 70 over here as well and the fifth edition answer is maximum hill angle is 24 degrees.