VIDEO TRANSCRIPT

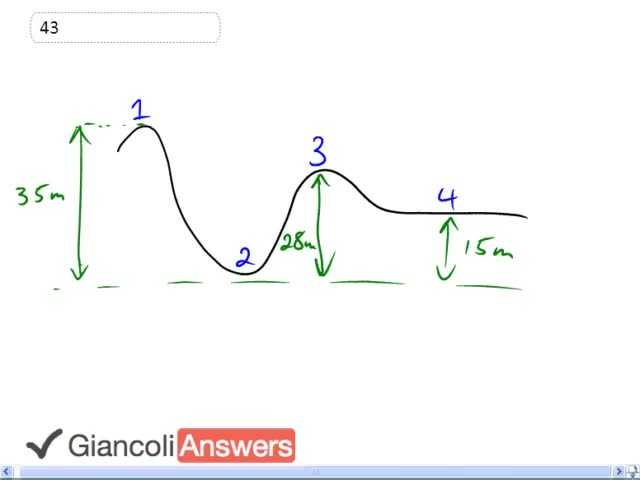
We are going to calculate the speed of this roller coaster at positions 2, 3, and 4, assuming it's at rest at position 1. And we'll do so by saying that energy is conserved, and we'll just actually be interested only in this change in height between position 1 and 3 and 4. That's just that change in height that's going to matter. And I'll show you what I mean. So we have initial kinetic and potential, adding up to the final kinetic and potential as always. And we know that the initial kinetic is 0. And then we'll substitute for this other things. We have 'mghi' that's the initial height of 35 meters. That's the gravitational potential that we start with. It's one half 'mvf' squared, plus 'mg' times whatever the final height is. Dividing through by the common factor 'm', and then bringing this term over to the left, by subtracting from both sides. And also multiplying everything by 2, to get rid of this fraction. And square rooting, in order to solve for 'vf'. We get 'vf' is, the square root of, 2'ghi' minus 2'ghf'. And we'll simplify that a little more to make it look cleaner. So we have 2'g' times 'hi' minus 'hf'. So we're going to use that formula, to calculate the speed in each of these positions. So at position 2, we have 2 times, 9.8 times, initial height of 35 meters, minus 0. The position 2 is the reference level so there has no height, there in position 2. So this becomes, 26 meters per second.

In part b, we'll find the speed of position 3, so it's going to be the square root of 2'g' times initial height, minus the height of position 3. And position 3 being, 28 meters. So we have square root of 2, times, 9.8 times, 35 meters, minus 28 meters. And so that answer is, 12 meters per second. And at position 4, we have 2 times 'g ' times initial height, minus the height of position 4. So we have 2 times, 9.8 times, 35 meters, minus 15 meters. And we get an answer 20 meters per second at position 4.