
- Given the vectors and shown in Fig. 3-35, determine .
- Determine without using your answer in (a). Then compare your results and see if they are opposite.
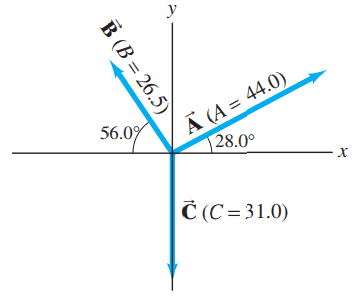
In order to watch this solution you need to have a subscription.
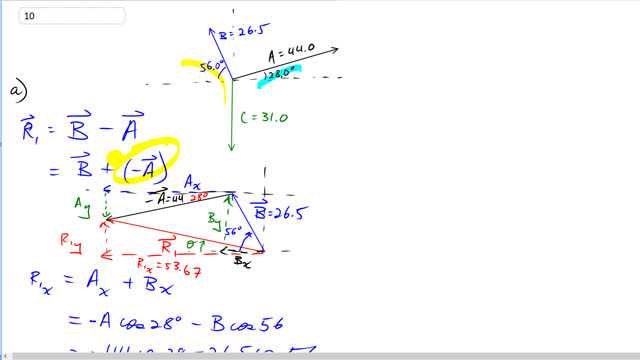
This is Giancoli Answers with Mr. Dychko. B minus A is the same as going B plus negative A and I would like to think of it that way because when you are drawing a vector then if you draw the negative of a vector, you are drawing it in the opposite direction but otherwise, same length and you know, same angle, just to the other side... just flip it over. So instead of 28 degrees above the positive x-axis, vector A the negative A is gonna be 28 degrees below the negative x-axis so it's gonna be as drawn here. And so we put the tail of negative A on the head of B and then the resultant goes from the very beginning which is at the tail of B to the very end which is at the head of vector negative A. And so we are finding the length and direction of this red vector R, that's the resultant. So B is 56 degrees above the negative x-axis we have negative A 28 degrees below the negative x-axis and well, let's start by finding the x-component of the resultant and it's gonna be the x-component of A plus the x-component of B. Now the x-component of A is found by the length of A times cos 28 and it's gonna be negative because it's to the left so it's negative 44 times cos 28 and then the x-component of B is also to the left and so it's also negative so minus 26.5 times cos 56 and we get negative 53.67 for x-component of the resultant. For the y-component, we'll take negative 44 times sin 28 and so for the y-component of A, it's gonna be negative since it's directed downwards and then we have positive 26.5— length of B—times sin of 56 and that gives us this y-component of B and we use sin because we are finding the component opposite to the angle and sin is opposite over hypotenuse so when we multiply by the hypotenuse times sin 56, we get the length of the opposite and we have 1.31. And then the length of the resultant then is using Pythgoras square root of 53.67 squared plus 1.31 squared giving us 53.686 and then the angle will be— now we are finding this angle Θ here for the resultant— it's gonna be the inverse tangent of the opposite length divided by the adjacent length so it's the inverse tangent of the y-component divided by the x-component of the resultant. And so it's inverse tangent of 1.31 divided by 53.67 and that gives us a resultant of 53.7 units, 1.4 degrees above the negative x-axis so it's slightly above the negative x-axis, okay. There. And then R 2 is gonna be A minus B so that's A plus negative B. So this is vector A here and then we add to that the opposite of vector B so that's the same line but just going in the other direction, this way and we'll put that on the head of vector A as shown here and that's 56 degrees below the positive x-axis when we put this in the opposite direction and that's what I have shown here. And to get the x-component then of the resultant which connects the beginning of A to the end of B, we have 44 times cos 28 that's the x-component of vector A plus 26.5 times cos 56 gives you x-component of B and we get 53.668 and then the y-component of the resultant in the second case, 44 times sin 28 minus 26.5 times sin 56 and that gives us negative 1.31 and Pythagoras and inverse tangent again and we get 53.7 units, 1.4 degrees below the positive x-axis and we confirm that these two vectors, R 1 and R 2 are opposites; they have the same length and we have one directed 1.4 degrees above the negative x-axis and so this is R 1. So that's 1.4 degrees above the negative x-axis and then we have R 2, same length directed 1.4 degrees below the positive x-axis; they are indeed opposites.
this is a mess
here's a more helpful video https://www.youtube.com/watch?v=DCIVs2ASxhk