A grasshopper hops along a level road. On each hop, the grasshopper launches itself at angle $\theta_0 = 45^\circ$ and achieves a range $R = 0.80 \textrm{ m}$. What is the average horizontal speed of the grasshopper as it hops along the road? Assume that the time spent on the ground between hops is negligible.

VIDEO TRANSCRIPT

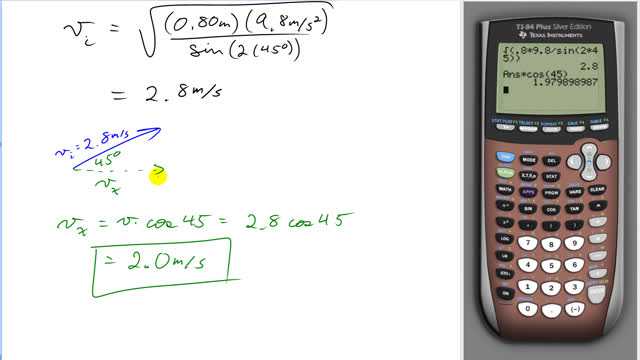
This is Giancoli Answers with Mr. Dychko. We'll use the range formula to figure out the initial velocity of the grasshopper and then knowing its angle is 45 degrees, figure out the x-component of its velocity and there we go. So we rearrange this to solve for v i squared and we'll times by g over sin of 2Θ both sides and then we get v initial squared equals Rg over sin 2Θ. Take the square root of both sides and we solve for the initial velocity and so that will be square root of 0.8 meters times 9.8 meters per second squared divided by sin of 90 because that's 2 times 45 and we get 2.8 meters per second. And then the horizontal component of its velocity is the adjacent leg of this right triangle here and so we use cosine 45 to figure that out. And we multiply 2.8 times cos 45 to get 2.0 meters per second is the horizontal velocity that's two significant figures since we had two significant figures in our range.