A passenger on a boat moving at 1.70 m/s on a still lake walks up a flight of stairs at a speed of 0.60 m/s, Fig. 3-43. The stairs are angled at $45^\circ$ pointing in the direction of motion as shown. What is the velocity of the passenger relative to the water?

VIDEO TRANSCRIPT

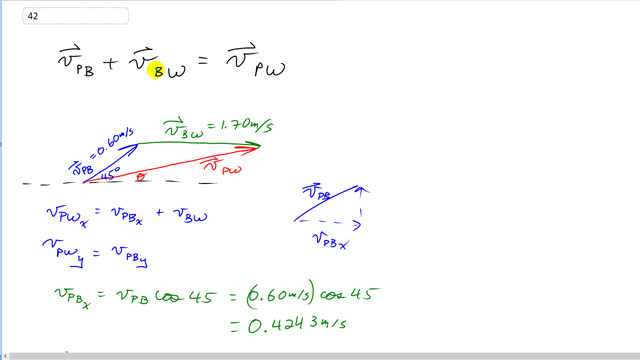
This is Giancoli Answers with Mr. Dychko. To find the velocity of the person with respect to the water, we'll have to add the velocity of the person with respect to the boat to the velocity of the boat with respect to the water and with the inner subscripts being the same, they will cancel away leaving us with the outer subscripts, P and W. So here's the velocity of the person with respect to the boat 45 degrees to the horizontal going at 0.60 meters per second climbing up the stairs and then we have velocity of boat with respect to the water straight horizontal—1.7 meters per second— and then in red we have the resultant which is velocity of the person with respect to the water. So the resultant has an x-component equal to the sum of the x-components of the vectors we are adding and the y-component of the resultant is the velocity of the person with respect to the boat in the y-direction and the velocity of the boat with respect to the water has no y-component because the boat's not going into the water nor is it levitating off the water. So we have velocity of the person with respect to the boat in the x-direction is the cos 45 times the 0.6 meters per second because the x-component is the adjacent leg of this triangle here and that gives 0.4243 meters per second and the y-component of the person with respect to the boat is v PB times sin 45 because it's the opposite leg and sin gives it the opposite leg of a right triangle when you multiply by hypotenuse and so it turns out to be the same; sin 45 equals cos 45 so we also get 0.4243 meters per second here. And then the x-component of the velocity of the person with respect to the water then is 0.4243 meters per second plus 1.70 meters per second which is 2.124. And in the y-direction we have this and then the magnitude of the velocity of the person with respect to the water is the square root of the sum of the squares of the components of the resultant and so that's square root of 2.124 meters per second squared plus 0.4243 meters per second squared and that gives about 2.17 meters per second. And then the angle Θ is the inverse tangent of the opposite divided by the adjacent and that gives you the angle with respect to horizontal and that's 11 degrees above horizontal.