
Three vectors are shown in Fig. 3-35. Their magnitudes are given in arbitrary units. Determine the sum of the three vectors. Give the resultant in terms of
- components,
- magnitude and angle with the +x axis.
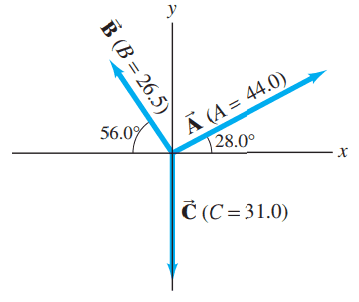
In order to watch this solution you need to have a subscription.
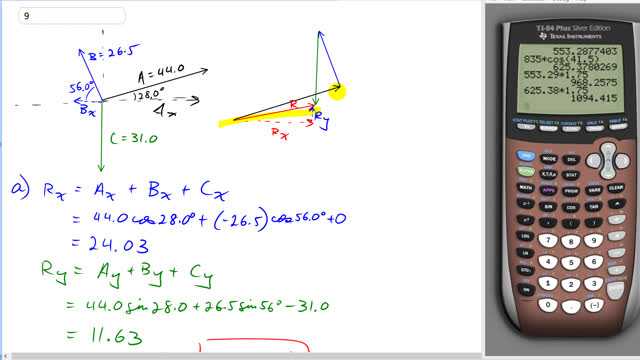
This is Giancoli Answers with Mr. Dychko. So here are the three vectors we are gonna add them together using the head to tail method. So first we'll place vector A down here and then on the head of vector A, we'll put the tail of vector B and that's vector B there. And then on the head of vector B, we'll put the tail of vector C and then we end up here as our destination. And so our resultant connects the very beginning to the very end so that's the red arrow here. And it has components R x along this line and R y this little blue part there. And so in the x-direction, we have A x plus B x plus C x. The x-component of A is gonna be its length 44 times cos of the angle above the x-axis—28 degrees— and then add to that the negative of 26.5 times cos 56 and it's negative because this component of B in the x-direction is to the left and it's the negative direction, say and there's no x-component at all for vector C since it's straight down not to the right or left at all and so we have resultant in the x-direction is 24.03. And for the y-direction, it's the same kind of story we find the y-components of each vector and vector A, we use 44 times sin of 28 and sin is opposite over hypotenuse and so just giving you an example of how that works. We have here's A y so we have sin of 28 equals A y over A and so multiply both sides by A and then you get A y equals A times sin 28 and so that's 44 times sin 28. And same idea with B, also upwards so also positive so plus 26.5 times sin 56 and then minus 31.0—minus because it's directed down for the y component of C— and there's no trig required since C is entirely downwards. And our final answer then is components of the resultant or 24.0 to the right and then 11.6 upwards and that's reflected by this picture here; we expected both to be positive. And then finding the magnitude and angle with respect to x-axis; for the magnitude of the resultant, we take the square root of the sum of the squares of the components. So that's the square root of 24.03 squared plus 11.63 squared and then that gives us 26.7 units and take the inverse tangent of the opposite divided by the adjacent and that gives 25.826 degrees above the positive x-axis.