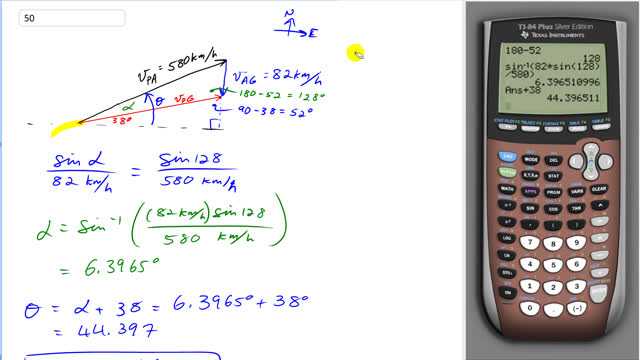
An airplane, whose air speed is 580 km/h, is supposed to fly in a straight path $38.0^\circ$ N of E. But a steady 82 km/h wind is blowing from the north. In what direction should the plane head? [Hint: Use the law of sines, Appendix A-7.]

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The resultant velocity of this plane has to be along the red line here directed 38 degrees north of east and the plane has to deal with this wind that's going 82 kilometers per hour from the north and the plane has an air speed of 580 kilometers per hour and has to be directed along some angle Θ that we need to figure out in order to make all this work. Now we wanna go sin of α— this angle that's inside the triangle here— divided by the length of the opposite side equals sin of this angle here divided by the length of its opposite side which is 580 and then we'll solve for α and then add α to 38 to get our answer Θ. Now this angle down here we can figure out by first knowing what this angle is this is our right triangle here and so we know 90 degrees and 38 degrees and so we have this angle here then is well these two have to total 90 since all three angles in the triangle make 180 so there's 90 here taking up already so that leaves 90 left for these two angles here and so the 90 minus the 38 in this bottom corner leaves 52 degrees for this angle. And then supplementary angles are along the straight line that means this angle inside the triangle here is gonna be 180 minus the 52 degrees up here which gives 128 degrees for this angle and so that's where we get the 128 here from. So now we can solve for α by multiplying both sides by 82 and we get then the α is the inverse sin of 82 kilometers an hour times sin 128 divided by 580 kilometers an hour which gives 6.3965 degrees right here and add to that 38 degrees gives about 44.4 degrees north of east.