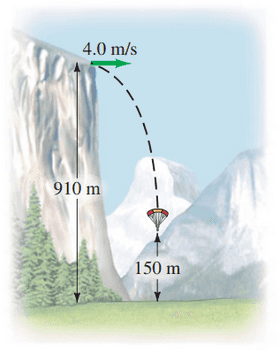
Extreme-sports enthusiasts have been known to jump off the top of El Capitan, a sheer granite cliff of height 910 m in Yosemite National Park. Assume a jumper runs horizontally off the top of El Capitan with speed 4.0 m/s and enjoys a free fall until she is 150 m above the valley floor, at which time she opens her parachute (Fig. 3-37).

VIDEO TRANSCRIPT

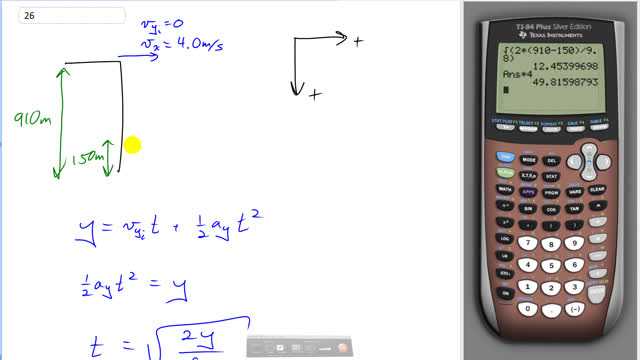
This is Giancoli Answers with Mr. Dychko. The El Capitan is 910 meters high and then this extreme sport base jumper I guess opens the chute when they are 150 meters above the ground— here's the ground. We'll take down to be positive, to the right positive; they launch themselves to the right with a speed of 4.0 meters per second and they have no vertical velocity initially and we'll first figure out how much time the jumper is in the air free falling before they open the chute so how long does it take to go from this height to this height here when they are 150 meters above? So we have vertical displacement is initial vertical velocity times time plus one-half acceleration in the vertical direction times time squared there's no vertical velocity initially so that term disappears and then we'll, you know, move this term to the left because it has the unknown t in it and then we'll multiply both sides by 2 over a y and then take the square root of both sides and on the left, the 2 and the a y disappear and they cancel away and on the right we have 2 times the vertical displacement divided by the vertical acceleration and take the square root of all that. The vertical displacement is the height of the cliff 910 meters minus the 150 meters distance that they are still above the ground and so it's this that we are trying to find here that's 910 minus 150 and that's what goes in here. And so we take the square root of 2 times that displacement divided by the vertical acceleration— 9.8 meters per second squared— and that gives 12 seconds in free fall. And then the distance from the cliff side when the chute opens is gonna be their horizontal velocity—4 meters per second— multiplied by the amount of time that they spend falling which is the amount of time that they spend going sideways too and this speed is constant because it's unaffected by gravity since it's perpendicular to gravity— acceleration only acts vertically. So their horizontal displacement will be the 4 meters per second times 12.454 seconds which gives 50 meters and instead of writing the number 50 meters like that I wrote 5.0 times 10 to the 1 in order to be clear that there are two significant figures in this number whereas if I wrote just 50, it would be ambiguous it's not, you know, strictly speaking this would be one significant figure the way it's written and so we have two significant figures here.