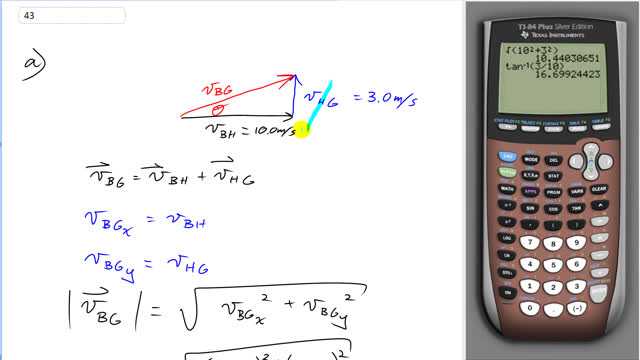
A person in the passenger basket of a hot-air balloon throws a ball horizontally outward from the basket with speed 10.0 m/s (Fig. 3-44). What initial velocity (magnitude and direction) does the ball have relative to a person standing on the ground

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The ball is launched horizontally in the reference frame of the hot air balloon at 10 meters per second and the hot air balloon is going upwards with respect to the ground at 3 meters per second and the question is what is the apparent velocity of the ball with respect to the ground or, in other words, what somebody standing on the ground, which makes them in the reference frame of the ground, observe for the ball's velocity? So it will be going somewhat to the right and somewhat upwards because it's being thrown to the right from the balloon and the ballon itself is going up. And so we add the velocity of the balloon with respect to the ground or sorry, we find the velocity of the ball with respect to the ground by adding the velocity of the ball with respect to the hot air balloon and plus the velocity of the hot air balloon with respect to the ground. I chose B to be the subscript for ball not the balloon because then I chose H to be the subscript to denote the hot air balloon. So the H's of the inner subscripts, they cancel leaving us with ball with respect to ground which is what we want. So the x-component of the ball with respect to ground's velocity is just the velocity of the ball with respect to the hot air balloon and because this velocity here has no x-component. And likewise with the y-direction, it's a little bit convenient because only the hot air balloon with respect to ground velocity has any y-component and so these two things together make up the components of our resultant. And so the magnitude will be the square root of the sum of the squares of the components of the resultant and so that's the square root of 10 meters per second squared plus 3 meters per second squared that gives about 10.44 meters per second. Then the angle Θ is the inverse tangent of the opposite divided by the adjacent and that gives us inverse tangent of 3 over 10 which is 17 degrees and according to this picture that's above the horizontal. In part (b), we get the same quantities except it's 17 degrees below the horizontal because these velocities are all the same except for the direction of the hot air balloon with respect to the ground is now downwards but the length of all these arrows are all the same and so we don't need to do with the calculations again; it's just 10.4 meters per second, 17 degrees below horizontal.