Suppose a vector $\vec{V}$ makes an angle $\phi$ with respect to the y axis. What could be the x and y components of the vector $\vec{V}$?

VIDEO TRANSCRIPT

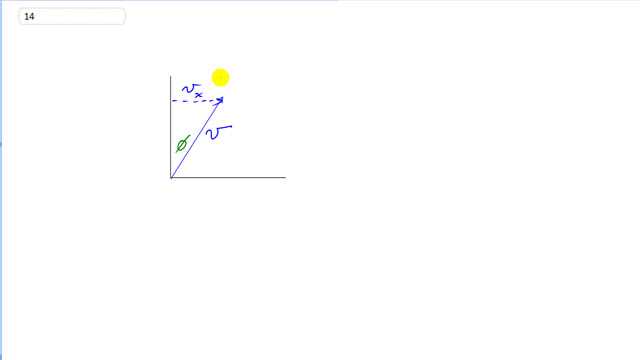
This is Giancoli Answers with Mr. Dychko. Here's vector V at an angle φ with respect to the y-axis. It's gonna have a x-component in the x-direction like this that's v subscript x and this is the opposite leg of the right triangle and so when you hear the word opposite, you should be thinking about sin because the sin of φ is the length of the opposite v x divided by the length of the hypotenuse v and so we can find the x-component by multiplying both sides by v and we get v x is v sin φ— oops not Θ, φ— and that's the answer there although it's slightly ambiguous the way they ask the question because it's possible that the angle φ could be on the other side of the y-axis in which case, the vector would be like this and φ would be in here and in this part (b), you would have to say that v x is the negative of v sin φ because it's going to the left there's v x. Okay. But keeping that in mind, the y-component is not ambiguous because it's with respect to the y-axis which you understand to be the positive y-axis, didn't say negative y-axis so we have here v y. The cos of—let's put this in a different color I guess— the cos of φ is adjacent over hypotenuse that's v y over v and multiply both sides by v and you get v y is v times cos φ and there's the y-component and here's the x-component. So when you are thinking about components, don't memorize the way to get it in terms of cos or sin because as you can see, it depends on how the angle is measured. So the x-component is typically found using the cos because it's more common to have your angle with respect to the x-axis but you can't always count on that being true and this question demonstrates that where sometimes the angle is with respect to the y-axis in which case, the x-component is found using sin; always draw a picture.