A person going for a morning jog on the deck of a cruise ship is running toward the bow (front) of the ship at 2.0 m/s while the ship is moving ahead at 8.5 m/s. What is the velocity of the jogger relative to the water? Later, the jogger is moving toward the stern (rear) of the ship. What is the jogger's velocity relative to the water now?

VIDEO TRANSCRIPT

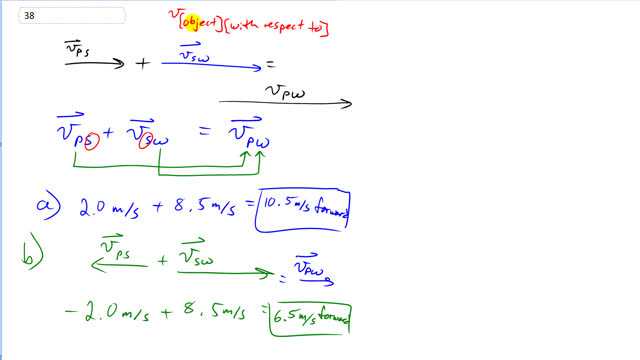
This is Giancoli Answers with Mr. Dychko. For relative velocity questions, it's really important to know what the order of the subscripts should be? The first subscript should be the object that you are interested in the velocity of and then the second subscript refers to the reference frame at what it's with respect to. So this first velocity here is the velocity of the person with respect to the ship and then we are gonna add to that the velocity of the ship with respect to the water. And then when you write it this way and you add these vectors, when you have the inner subscripts being the same— so the S here matches the S here— they disappear and you end up with the velocity of the person with respect to the water and you have the outer subscripts that go into your answer. And anytime you need to flip the subscripts around, if this was v SP and you wanted v PS, you could always put a negative in front of it and that switches the direction around. Okay. So velocity of the person with respect to the water then is the velocity of the person with respect to the ship which is 2 meters per second to the right we'll call that forward and add to that 8.5 meters per second velocity of the ship with respect to the water and we get total of 10.5 meters per second velocity of the person with respect to the water forwards. And now when the person is walking backwards towards the stern, the velocity of the person with respect to the ship is negative now it's in the, well, we defined forward or positive to be to the right that makes the velocity of the person with respect to the ship negative in part (b), negative 2 meters per second plus the velocity of the ship with respect to the water giving us 6.5 meters per second forwards. So the person is still going forwards with respect to the water even though they are walking backwards because the ship is moving forward so much faster than they are walking backwards.