You are here

Select a problem

Question:

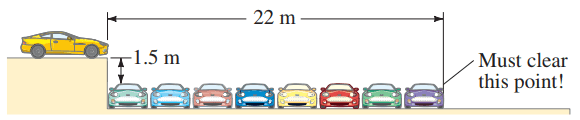
A stunt driver wants to make his car jump over 8 cars parked side by side below a horizontal ramp (Fig. 3-41).

With what minimum speed must he drive off the horizontal ramp? The vertical height of the ramp is 1.5 m above the cars and the horizontal distance he must clear is 22 m.
If the ramp is now tilted upward, so that "takeoff angle" is $7.0^\circ$ above the horizontal, what is the new minimum speed?

Problem 37.

Figure 3-41.

Source: Giancoli, Douglas C., Physics: Principles with Applications, 7th Edition, 2014.

Quick Answer:

$4.0 \times 10^1\textrm{ m/s}$
$24 \textrm{ m/s}$

Giancoli 7th Edition, Chapter 3, Problem 37

(6:40)

Chapter 3, Problem 37 is solved.

View sample solution

Transcript for this Giancoli solution

This is Giancoli Answers with Mr. Dychko. In part (a), this stunt driver is gonna drive off a horizontal cliff basically and clear this 22 meters horizontally with a drop of only 1.5 meters; he can only drop 1.5 meters if he's gonna clear all the cars that are stacked below here so the horizontal speed is the question. The vertical initial speed of this car is zero because he's driving straight horizontally, there's no angle here yet, we'll consider an angle of 7 degrees in part (b) of the question and the vertical displacement is negative 1.5 meters because we'll take up to be positive direction and right to be positive. So first we'll find out how much time it will take to reach this 22 meter position here and then knowing that time, we'll figure out what speed the car will need to have. in order to get there that time. So the height is known; the change in height or the vertical displacement is negative 1.5 meters and the initial y-component of velocity is zero. So we'll find time using this formula, we'll multiply both sides by 2 and divide by a and then take the square root of both sides to find time and that's the square root of 2 times negative 1.5 meters—displacement— divided by negative 9.8 meters per second squared— acceleration— and we get 0.5533 seconds. So the car needs to cover this 22 meters horizontally in that 0.5533 seconds and the horizontal distance traveled will be the horizontal speed times time and divide both sides by t and we switch the sides around and we get v x is the distance 22 meters divided by the time of 0.5533 seconds and so the car needs a speed of about 40 meters per second and I wrote it in scientific notation here just to be clear that there's two significant figures there since we had two significant figures in the numbers that we are starting with. In part (b), the car takes off on a bit of an angle— 7 degrees above the horizontal. And so we expect their required speed to be a little bit less because the car's going to spend more time in the air as a result of this initial upwards velocity that it has. So first we'll figure out the time that it spends in the air although we are not gonna get a number, we are just gonna get an expression for it in terms of the horizontal distance and the velocity which we don't know yet. So the horizontal distance covered is v x times t but v x is now an expression in terms of this speed and the angle of takeoff Θ and v x is the horizontal component of velocity and it's the adjacent leg of this triangle here and so it's v times cos Θ and so we'll substitute that in for v x and so x is v cos Θ times t and then solve for t by dividing both sides by v cos Θ and we get t is horizontal displacement x divided by v cos Θ. And that's gonna be useful in the next equation where we have this known height y equals the initial y velocity times time plus one-half at squared and we'll substitute for t in both places here using what we found before knowing t in terms of x and v and Θ. And then we'll substitute for v y initial and that's v sin Θ because the y-component of the velocity is the opposite leg of this triangle and so we use sin to get that multiplied by v and also substitute for a which is negative g. Alright and then a few magical things happen here; we get the v's canceling from this first term and sin over cos can be written as tan Θ; that's just for convenience, you don't have to do that but it's easier on the writing just to write tan Θ instead of sin Θ divided by cos Θ. And then minus g times this whole thing squared over 2 and we get that and then we'll move this term to the left hand side because it contains the unknown that we wanna find v and then move the y to the right hand side and we get g x squared over 2v squared cos Θ squared equals x tan Θ minus y and this unknown v is in the denominator so we need to move it into the numerator by multiplying both sides by this whole denominator and I guess that moves it to the right hand side— which is kind of counterproductive but anyway certainly getting it out of the denominator is a good thing. So we are multiplying both sides by this and it disappears from the left side leaving us with g x squared on the left side and on the right hand side, we'll just put the whole thing in bracket's times 2v squared cos Θ squared. And now we'll divide both sides by everything here except for the v so we are dividing both sides by 2 times x tan Θ minus y, all in brackets, times cos Θ squared and then take the square root of both sides to solve for v and it looks messy but it's true; we have this v is the square root of 9.8 meters per second squared times 22 meters squared divided by 2 times—let me get the calculator on here— divided by 2 times 22 meters times tan of 7 degrees minus negative 1.5 meters. So y-displacement is downwards and so it's negative 1.5 meters and we chose up to be the positive direction times cos squared 7 degrees and here's how to punch it into the calculator making sure you get your bracket matching correct there and we have about 24 meters per second is the required minimum takeoff speed and you will notice that this is about almost half of the required speed as it had in part (a) with only a small 7 degree incline.

Comments

By kmoons25 on Mon, 11/07/2016 - 20:00

why do you do these things?

By Mr. Dychko on Tue, 11/08/2016 - 00:54

Hi kmoons25, Well, I know physics can be confusing. When you have a more specific question, just let me know.

All the best,
Mr. Dychko

By idan on Fri, 03/03/2017 - 13:55

I originally tried using the Range formula which gave me a slightly wrong answer. I'm assuming it's not applicable in this situation because of the 1.5 m drop?

By Mr. Dychko on Sun, 03/12/2017 - 12:53

Hi idan, yes you're exactly right. The range formula was derived using the assumption that the final and initial heights are the same. Since that's not the case here, as you say, the range formula doesn't apply.

Cheers,
Mr. Dychko

By suriyak786 on Sat, 03/11/2017 - 20:04

For part b why didn't we also find out Vx. Why did we find Vy

By Mr. Dychko on Sun, 03/12/2017 - 13:17

Hi suriyak786, thank you for your question. At 3:20 we made use of $v_x$ to create an expression for $t$ in terms of things that we know, such as $x$ and $\theta$, and the one thing we don't know, $v$. That was then substituted into the vertical displacement formula, which only has $v_y$ in it since only the vertical component of velocity affects the vertical displacement of the car. Does that help?

All the best,
Mr. Dychko