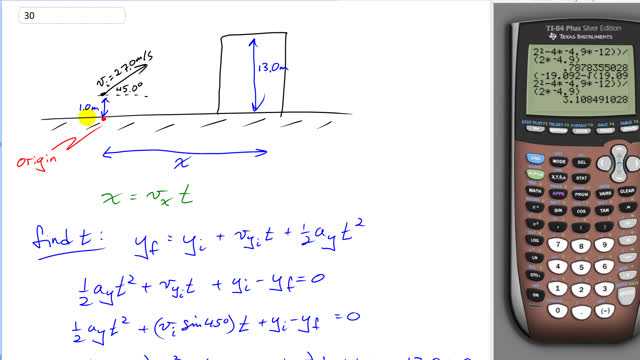
A baseball is hit with a speed of 27.0 m/s at an angle of $45.0^\circ$. It lands on the flat roof of a 13.0-m-tall nearby building. If the ball was hit when it was 1.0 m above the ground, what horizontal distance does it travel before it lands on the building?

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. Here's a good example of a question where you want to find the range of a projectile but you cannot use the range formula; range formula is only when the projectile lands at the same height that it started with and that's not the case here. This projectile is gonna start at a height of 1 meter and then it's gonna go up and then down and then land on top of this building, on the roof. So we are gonna choose the origin to be here on the ground directly below the projectile and that means the projectile starts at a position of positive 1 meters and we'll take up to be positive and right to be positive and we are gonna calculate the range by going the horizontal component of the velocity multiplied by the time that it spends in the air and horizontal component of the velocity we can find by going v x equals the initial velocity— 27.7—times cos 45 degrees. and the time, on the other hand, is a little bit more complicated to figure out and so that's what this next bit of work is all about. So vertical position, we don't often write this formula with the y initial in there because typically we choose the origin such that y initial is zero but in this case since we are given two different heights both with respect to ground, we might as well take the ground to be the y equals zero height. So that means y final is 13 and y initial is 1. So we have y final is y initial plus vertical component of the velocity initially times time plus one-half times vertical acceleration times time squared. We are gonna solve this for time to get the amount of time this ball spends in the air so we can multiply v x by that time to get the range x. So we'll subtract y f from both sides and then we'll turn this into a quadratic equation here and vertical component of the velocity can be substituted with initial velocity times sin 45 because the vertical component of the velocity is the opposite leg of this right triangle here and you use sin to get the opposite leg and then we have y initial minus y final and then substituting in some numbers, we have one-half times negative 9.8 meters per second squared— that's the acceleration vertically due to gravity plus times time squared plus 27.0 meters per second times sin 45 plus 1 meter minus 13 meters and you end up with this that you can plug into the quadratic formula. And you notice that you get two positive answers and you have to choose the one that makes the most sense so we have to look at our picture to figure out which makes sense. So this formula doesn't understand the question all this formula does is tells you at what time will the projectile reach the final height of 13 meters and it will do it twice it will get to 13 meters on the way up, it's here at the building height level and then as it continues in this parabola it will land on the roof here and it will be at the 13 meter height again and this second instance, where the ball is at 13 meters, is the time we want and that's the larger time so we are gonna choose 3.108 seconds as the time to use here. We know that it took this arc because, you know, it can't land on the building when it's on its way up, it can only land on the building's roof when it's on its way down. Okay. So we can plug things into this horizontal range equation now; we have 27.0 meters per second times cos 45, this gives the horizontal component of the velocity so v x initial I guess you could say or v x because you know, there's no initial or final business here since horizontally the velocity is constant and multiply that horizontal component of the velocity by the time— 3.108 seconds— and that gives us times cos 45 gives us 59.3 meters.