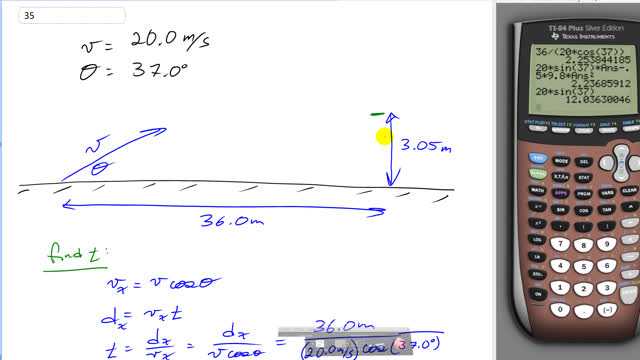
Suppose the kick in Example 3-6 is attempted 36.0 m from the goalposts, whose crossbar is 3.05 m above the ground. If the football is directed perfectly between the goalposts, will it pass over the bar and be a field goal? Show why or why not. If not, from what horizontal distance must this kick be made if it is to score?

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. This field goal kick is made at 20 meters per second at an angle of 37 degrees to the horizontal and it's 36 meters away from the goal post and the crossbar is 3.05 meters above the ground and our question is once this ball gets to this position—horizontally— will it have a height greater than 3.05; will it make it over the crossbar? So first we'll find out how long it takes to get from here to here which we can do using the horizontal velocity of the ball and then after we know that time, we'll figure out what its height will be. So the horizontal component of its velocity is v times cos Θ because v x is the adjacent leg of this right triangle here and so adjacent there means cos and so the horizontal distance that it travels we know is gonna be the horizontal speed times time—there's no acceleration horizontally—and so from this we can figure out the time it takes to go this known horizontal distance of 36 meters and so we divide both sides by v x here and we get the time is the horizontal distance divided by horizontal component of its velocity. So that's 36 meters divided by 20 meters per second times cos 37 which gives 2.2538 seconds. So what will its height be at that time we'll use this formula to figure that out; the height will be the initial y-component of its velocity times time plus one-half times the acceleration times time squared and the vertical component of its velocity is v times sin Θ because v y is the opposite leg of this triangle and we use sin to figure that out and then we substitute v sin Θ in for v y initial and negative g in place of the acceleration because upwards is the positive direction so we have a negative sign in front of the g there since the acceleration is downwards. And so we have 20 meters per second times sin 37 times the time that we figured out when it gets to a horizontal position of 36 meters plus one-half times negative 9.8 meters per second squared times the time squared and that gives 2.24 meters will be its height there and that's less than 3.05 meters and so there's no field goal; the ball will cross underneath the cross bar. So to figure out the range of distances where the kicker could be such that the ball would be above 3.05 meters, we'll figure out the times when the ball is actually at that height of 3.05 meters and so it's gonna be at that height twice; it's gonna be at that height on the way up and so the ball goes in an arc like this and the ball is gonna be above this height at this time and then again at this time and so basically, if the crossbar's anywhere between here and here, the field goal would count and well, we are not gonna move the crossbar though but we are gonna move the kicker so that the kicker moves this whole arc so that it's like this somewhere in between here and here; the kicker can go anywhere along there so that the arc is above the crossbar. Okay. So first we'll find out at what times it will be above that height—3.05 meters— and then knowing those times, figure out the horizontal distances. So the height is this formula—y initial t plus one-half a t squared and we'll subtract h from both sides and get our formula looking like this substitute in negative 9.8 meters per second for A and substitute for v y initial using sin 37 this time instead of cos and then we plug all this into our quadratic formula and so we have negative of the coefficient of the linear term so that's negative 12.04 plus or minus we are gonna actually use both this time so plus the square root of B squared so B is this coefficient here and minus 4 times the coefficient of the squared term so negative 4 times negative 4.9 times this constant term, the 3.05— minus 3.05— close the square root, close the numerator of this whole thing divide by 2 times A so that's negative 4.9 and we get 0.2868 seconds—that seems rather short that's what it is though. Okay and then we'll do the whole thing again 2nd function "Entry" to get the same stuff popping up and just put a minus sign in there and enter and we get 2.1703 seconds. And then we'll plug that into our times here and the close, the near position will happen when we have the smallest time so that's 0.2868 seconds and then the far position at 2.1703 seconds and so the distance will be somewhere between the answers to these two things; that's 20 times cos 37 times 0.2868 so that's 4.58 meters and 20 times cos 37 times 2.1703 seconds 34.7 meters. So anywhere between 4.6 meters away or 34.7 meters away, this will be a field goal.