
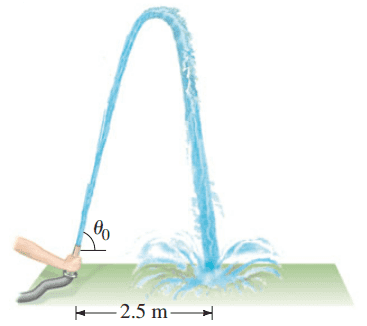
A fire hose held near the ground shoots water at a speed of 6.5 m/s. At what angle(s) should the nozzle point in order that the water land 2.5 m away (Fig. 3-36)? Why are there two different angles? Sketch the two trajectories.

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We can use this handy range formula to answer this question we know that the range because because this water lands at the same height that it started with and that's why we can use the range formula by the way, you can't use the range formula when the final height is different from the initial height but in this case, it's on the level so we use the level range formula. So the range is the initial velocity squared times sin of 2 times the angle that it was launched at divided by g—acceleration due to gravity. So we can times by g over v initial squared and solve for sin 2Θ and then take the inverse sin of both sides to get 2 times Θ is the inverse sin of the range times g divided by v i squared. And 2Θ then is the inverse sin of 2.5 meters—range— times 9.8 meters per second squared divided by 6.5 meters per second all squared and that gives 35.44 and it also gives 144.56 degrees. When you have the inverse trig function, there's actually an infinite number of solutions always but typically in Physics, we are most often interested only in the first answer that you get from your calculator; the calculator always gives answers that are the smallest positive answer that it could possibly give and I have labeled each of the quadrants here with cos, all, sin and tangent to tell you which quadrant's the different trig functions are positive in. So your calculator will usually give you an answer in here if you take the inverse sin, inverse cos or inverse tangent of any positive number, you will always get answer less than 90 and then it's your job to get all the rest of the answers, in case you need more. and this is one of those special questions where you actually do need one of the other answers. And it turns out you need the answer that's in this quadrant where sin is also positive. So when you take the inverse sin of this positive number, whatever that is, it turns out that there's two angles that meet that description of having that as their sin and explaining this in a lot of detail is like a whole another video but I have drawn a unit circle here to show that this sin is positive both here and here; sin is defined as the y-coordinate of a point on the unit circle and we normally think of it in terms of a triangle, opposite over hypotenuse but that's a sort of, you know, grade 11 type of definition for it and more sophisticated explanation is that it's the y-coordinate of a point on the unit circle and so there's two two points on this unit circle that have sin which is positive— this one and this one— and so what are the angles to those points that's what the calculator will tell you, it will tell you the angle to the first point here—35 degrees— and then the angle to the second point is gonna be 180 minus 35 so this 35 degrees is called the reference angle and you have 180 minus that 35 to get the next 144.56 degrees. And we know that we need this because we are interested in all answers for Θ that are less than 90 and these numbers are what 2Θ is equal to. So we have to divide both of them by 2 and we see that we get Θ is 18 or 72 degrees and here's a picture of the football or the water, sorry, being shot up at 18 degrees, it will get a range of 2.5 meters and at 72 degrees, it will just go a lot higher and spend more time in the air with a compensatingly less horizontal velocity though and they end up at the same range anyway.
I'm a bit disappointed I paid for this. You're rushing and half explaining everything.
It would be so much more helpful if you wrote out the solution as you went along, not scroll your mouse over your work half explaining it - especially the vector section.