
A diver running 2.5 m/s dives out horizontally from the edge of a vertical cliff and 3.0 s later reaches the water below. How high was the cliff and how far from its base did the diver hit the water?
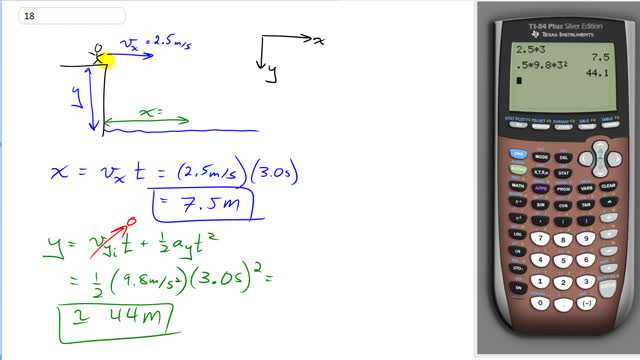
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This diver runs out off the cliff at 2.5 meters per second to the right and they hit the water 3 seconds later and the velocity to the right will be unchanged by gravity because gravity is acting only up and down and so that's a constant velocity to the right of 2.5 times 3 seconds gives a distance of 7.5 meters from the base of the cliff when they land. And the height of the cliff is given with this formula where we know the initial y-component of the velocity is zero and then we have plus one-half at squared where acceleration is that due to gravity and we are taking down to be positive here so we got positive 9.8 and then 3 seconds—the time squared— and then we get 44 meters is the height of the cliff.
should the answer not be 14.1 m if the s^2 gets cancelled?
Hi hockey11, thanks for your question. The answer is definitely , as shown, and not . I think the equation you're looking at is , is that right? It's correct that the units cancel, as you say. However, the numbers do not cancel. This means the calculation is with units of since the units cancel.
I hope this helps,
Mr. Dychko
Can you please explain why the acceleration in this question is assumed to be positive while it was negative in question #17? Thanks.
Hi sheumangutman,
Thanks for the good question. Choosing whether the upward or downward direction is positive is called "choosing a coordinate system". Choosing a coordinate system is something you do for every solution, and the choice is a matter of personal preference. The only rule is that you're consistent, which means if you choose the downward acceleration to be positive, then it means downward velocity also must be positive, and the same goes for downward displacement. I choose down to be the positive direction since it meant there were no negative signs in my work, which I think looks just a little cleaner. The question is asking only for distances anyhow, which are positive, so I might as well make my calculations result in the final answer, rather than finding a negative downward displacement (which would have happened if I made the more conventional choice of upward being positive for the coordinate system) and then taking it's "magnitude" to get the final positive answer for height of the cliff.
Hope that helps,
Mr. Dychko
Hi, as the question asked how far from its base shouldn't the answer be square root (x ^2+y^2)? (displacement between landing point and the jump point)
Hi choianchoi, actually, since the question uses the word base, it's referring to the bottom of the cliff. The bottom of the cliff is the base of the cliff, so the question is asking only for the horizontal component of the displacement from the jump point to the landing point.
Hope that helps,
Mr. Dychko