
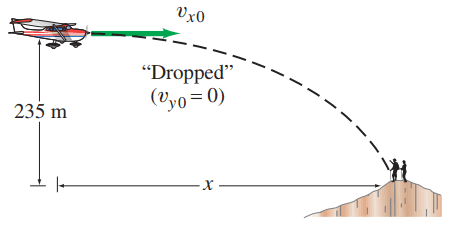
A rescue plane wants to drop supplies to isolated mountain climbers on a rocky ridge 235 m below. If the plane is traveling horizontally with a speed of 250 km/h (69.4 m/s), how far in advance of the recipients (horizontal distance) must the goods be dropped (Fig. 3-38)?

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This rescue plane is flying horizontally with a speed of 250 kilometers an hour and we'll convert that into meters per second so 250 kilometers per hour times 1 hour for every 3600 seconds makes the hours cancel and then times by 1000 meters per kilometer makes the kilometers cancel leaving us with meters per second and this is the same as dividing by 3.6 so that's what you see in my calculator then we have 69.44 meters per second. Okay it's at a height of 235 meters above the mountain climbers and what is this distance away that it has to drop a payload out in order to have the supplies reach the mountain climbers? So we'll find x by going x equals horizontal velocity times time but we need to know what this time is and we'll get that by knowing that it is dropped from this height of 235 and its initial y-component of its velocity is zero because it's just dropped; it's not thrown down nor upwards and we can solve this for t after we get rid of this term, we can multiply both sides by 2 and divide by a y and then take the square root of both sides and we end up with this line. And so the time it spends near is the square root of 2 times 235 meters divided by 9.8 meters per second squared; displacement and acceleration are both positive because we chose down to be the positive direction and to the right to be positive as well and that gives 6.92526 seconds in the air and then x then is the horizontal component of its velocity times the amount of time it spends in the air which is 481 meters away then.