
Show that the time required for a projectile to reach its highest point is equal to the time for it to return to its original height if air resistance is negligible.
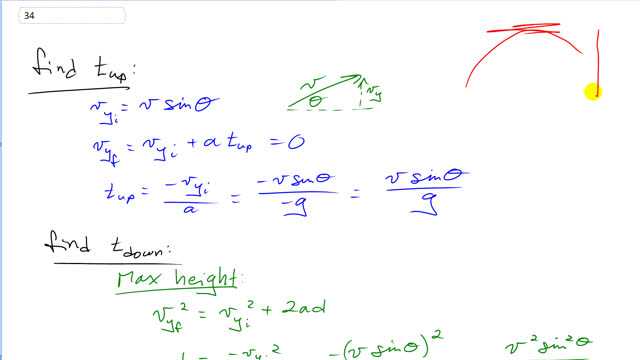
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We are going to first find the time it takes for the projectile to get to the top of its parabola up here and then we'll calculate the amount of time it takes to come back down and then compare the two and show that they are equal. So the projectile is launched at this angle Θ with some initial speed v and the y-component of its velocity then is v times sin Θ because this is the opposite leg of this right triangle and we'll find the time it takes to go up by using this formula that the final velocity equals initial velocity plus acceleration times time knowing that the final velocity is zero because it comes to a stop at the very top of its arc. And we'll subtract the intial speed from both sides and divide both sides by a and we end up with this; the time to go up is negative of the initial velocity divided by acceleration acceleration is g in the negative direction, downwards and then we'll substitute v sin Θ in place of the y-component of the velocity and then we end up with v sin Θ over g is the time it takes to go up. And now let's calculate the time it takes to go down and we'll do that by first figuring out what maximum height the projectile reaches and then calculate the amount of time it takes to fall from that height. So here's the formula that says the final y-velocity squared equals the initial y velocity squared plus 2a times displacement and displacement here is gonna be the height that we get to and well, we know that final velocity is zero again and we'll subtract y-component squared from both sides and then divide both sides by 2a to get this line here and substitute for what the y-component is in terms of the initial velocity and then we see that the negatives cancel and we have v squared sin squared over 2g is the maximum height. and so the next question is, how long will it take to fall from that height? And so we have this formula here to help us and we know that the initial velocity is zero because now we are considering falling from this maximum height so it starts from rest and then falls so initial velocity is zero now and we'll multiply both sides by 2 and divide both sides by a and switch the sides around so we have the unknown t down on the left—I didn't write the down here but I suppose I could— and we'll substitute for a which is negative g and then we'll also substitute for d which we calculated up here which is v squared sin squared over 2g and then put a negative in front of it because now it's a displacement so it's downwards and we have defined up to be the positive direction— didn't explicitly say that but that's what you always assume if nothing is otherwise stated— and then we have the 2's canceling and the negative's cancel and we have the time squared down is v squared sin squared over g squared and then take the square root of both sides and you have t down is v sin Θ over g which is the same as the time up v sin squared Θ over g and so time up is equal to time down.