
A tiger leaps horizontally from a 7.5-m-high rock with a speed of 3.0 m/s. How far from the base of the rock will she land?
In order to watch this solution you need to have a subscription.
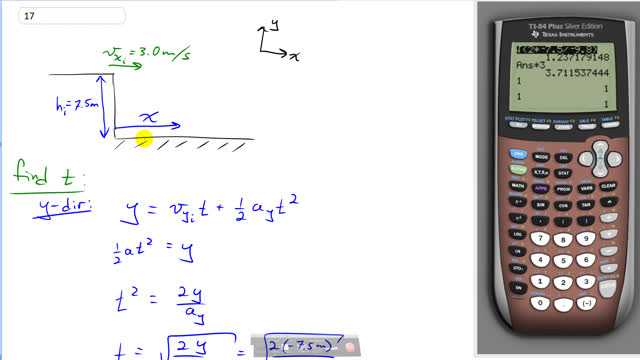
This is Giancoli Answers with Mr. Dychko. This tiger is leaping to the right off the cliff and the speed that it has to the right will be constant during its fall because the acceleration due to gravity affects only its vertical component of its velocity and so the horizontal one will stay the same. And we need to consider the vertical direction to know how long the tiger will be in the air and then we'll multiply that amount of time by its constant 3 meters per second velocity to the right to figure out how far it will go. So let's first figure out length of time it takes to fall 7.5 meters and we'll use this formula here; the initial component of the y velocity is zero and so we'll get the total vertical displacement equals one-half at squared and we'll find time by multiplying both sides by 2 over a and then we get this and then we take the square root of both sides to figure out the time. And that's the square root of 2 times the displacement which is negative 7.5 meters divided by the acceleration which is negative 9.8 meters per second squared that gives 1.2372 seconds and then that's the time that we multiply by the constant horizontal velocity of 3 to get a total distance of 3.7 meters to the right from the base of the cliff when the tiger lands.
Hi.Sr. I would like to know when the gravity is positive or negative
Hi joeotilio25, thanks for your question. Gravity is a force, just like any other, and it's sign depends on how you've chosen to define your coordinate system. Traditionally, positive is chosen to be upwards, which makes any vector pointing downward, be it velocity, displacement, acceleration, or force, negative when pointing down. In that coordinate system, the force of gravity would be negative since it's pointing down. So, gravity is negative in a coordinate system where up is positive, and gravity is positive in a coordinate system where down is chosen to be positive.
Hope this helps,
Mr. Dychko
Hi Sr. I am wondering what happened to the other "Y" when you were solving for time. It's the part where t = square root of 2Y/AY.
Hello, thanks for the question. The "y" in the denominator is just a subscript for the "a" (acceleration), to label the acceleration as "the acceleration in the y direction". It is not a separate factor, but maybe I wrote it a bit too big. The equation is .
All the best,
Mr. Dychko
Perfect, thank you.