
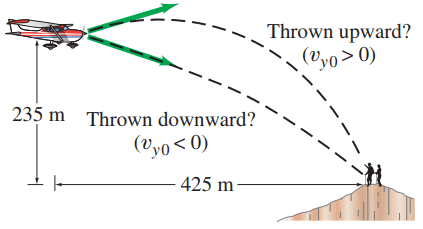
Suppose the rescue plane of Problem 31 releases the supplies a horizontal distance of 425 m in advance of the mountain climbers. What vertical velocity (up or down) should the supplies be given so that they arrive precisely at the climbers' position (Fig. 3-39)? With what speed do the supplies land?

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This plane is a known distance horizontally away from these mountain climbers of 425 meters and this is when it either throws the package down or throws it up with whatever speed is needed in order to have the package land at the mountain climbers given that it's released at this point. And the plane is 235 meters above the mountain climbers and it's traveling with this speed, 250 kilometers per hour converted into meters per second, is 69.44 meters per second. So we'll take down to be positive and to the right positive and we know how long the package spends in the air using this formula to say that the horizontal distance that the package covers equals its horizontal component of its velocity which doesn't change throughout its travel because acceleration due to gravity only affects the vertical component of the velocity So the horizontal distance it covers is v x times t and so we'll divide both sides by v x to solve for t. So t is 425 meters divided by 69.44 meters per second which is 6.1204 seconds. So that's the time that we can plug into this formula for the vertical displacement. We know what the vertical displacement is —it's 235 meters— and we know the time now and we know the vertical acceleration so we can solve this for v y initial the initial y-component of the velocity that it needs in order to land here. So we'll subtract one-half a yt squared from both sides giving us y-component initially of the velocity times time equals y minus one-half a yt squared and then divide both sides by t and you get this line and then that's 235 meters minus 0.5 times 9.8 meters per second squared times 6.1204 squared divided by the time gives 8.406 meters per second. Now that's positive and in our coordinate system, we define down to be positive so that's 8.406 meters per second down although I don't suppose we should have so many significant figures maybe three so let's call it 8.41 meters per second downwards. Alrighty. So what is the speed when it lands at the mountain climbers? So the speed will be or the magnitude of the velocity, in other words, is the square root of the sum of the squares of the components of the velocity so we are using Pythagoras here and we know what v x is already— that's the speed of the plane— and we have to find v y at this time 6.1204 seconds when it lands at the mountain climbers. So the y-component of velocity will be the initial y-velocity plus acceleration times time. So that's 8.4062 meters per second plus 9.8 times the time, 6.1204 seconds, which is 68.386 meters per second. So the speed then will be the square root of the horizontal speed squared plus the vertical speed squared which gives 97.4 meters per second which is really fast; and well, here I first want to show you what I plugged in I don't know if you guys get that much out of this calculator business but maybe you do so I'll just do it anyway. So there's the 97.—I guess it should be 5— and then times by 3.6 to turn it into kilometers per hour in order to understand that this is a really fast speed; that's 351 kilometers an hour and so this better be a well-packaged set of supplies.