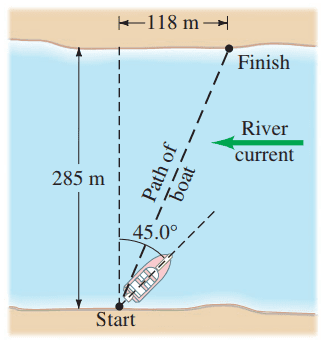
A boat, whose speed in still water is 2.50 m/s, must cross a 285-m-wide river and arrive at a point 118 m upstream from where it starts (Fig. 3-45). To do so, the pilot must head the boat at a $45.0^\circ$ upstream angle. What is the speed of the river's current?

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The velocity of the boat with respect to the water is at an angle of 45 degrees with respect to the shore here at 2.5 meters per second and combine that with the velocity of the water with respect to the shore, and you get this resultant, velocity of the boat with respect to the shore. And this resultant velocity is gonna be on the same line as the displacement so the displacement is gonna be along this line to from the starting point connecting the ending point and this end point is 118 meters downstream from where or upstream, I should say, from where the boat started and it goes 285 meters to get across the whole thing and we are gonna take a solve the triangle type approach to this question; we are gonna use the sin law and there's lot's of different ways to solve this question but this may not be the way you have chosen to do it yourself but I'm intentionally doing it that way just to show you some other approaches you could use. So we are going to figure out the length of this green arrow; that's the whole question, that's the velocity of the water with respect to the shore. And we know a few things; we know this angle in here is 45 degrees because we have this shore and this velocity of the water with respect to the shore parallel and this is a known angle of 45 and this is a parallel line rule called interior opposite angles are equal and so this is the transverse connecting to parallel lines and so this angle right here is 45 degrees. And then we have to figure out what Θ is and then once we know Θ, we can find this angle in here and I'm gonna call that γ and once we know that, we can use the sin law because we'll have all the angles known and one of the sides known and we can figure out this other side. First we'll find α here so we'll find α which is this angle in the displacement triangle and it equals the inverse tangent of the opposite over the adjacent 118 meters over 285 meters and that gives 22.49 degrees and then we'll find Θ which is this full 90 degree angle here minus the α we just figured out minus the 45 that we know from here and that gives 22.509 degrees for Θ which is an angle inside the triangle there. And then we know velocity of the water with respect to the shore divided by Θ or sin of Θ so a side divided by the sin of the angle opposite—that's sin— equals any other side divided by the sin of the angle opposite it. So we have v, velocity of boat with respect to the water divided by sin of γ. Now γ is 180 degrees which is the total of all three angles inside any triangle minus the 45 degree angle that's known there minus the angle Θ that we just found so it's a 180 minus 45 minus 22.509 gives γ, 112.491 and so then we'll rearrange this now to solve for v WS. And we'll multiply both sides by sin Θ and we have v WS is v BW sin Θ divided by sin γ. So that's 2.50 meters per second times sin 22.509—let's figure that out— sin 22.509 divided by sin of 112.491 and that gives 1.036 or about, I don't know, how many significant figures should we have here... looks like about... three I suppose although the angle... yeah the angle's are in three significant figures so that's 1.04 meters per second is the velocity of the water with respect to the shore; that's the speed of the current.