If $V_x = 9.80 \textrm{ units}$ and $V_y = -6.40 \textrm{ units}$, determine the magnitude and direction of $\vec{V}$.

VIDEO TRANSCRIPT

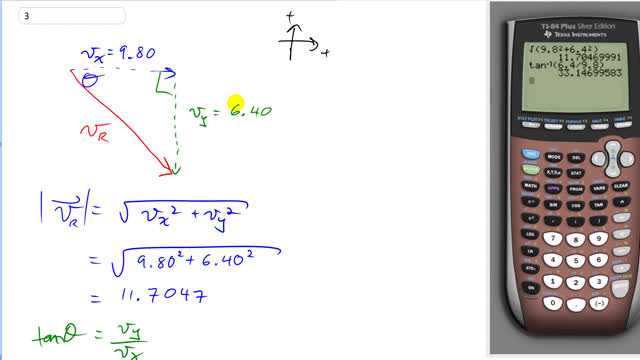
This is Giancoli Answers with Mr. Dychko. The x is 9.8 units to the right and we'll take the right to be positive and upwards to be positive and v y is negative 6.40 units so that's 6.40 units downwards and the resultant connects the origin to the end result and the magnitude of the resultant will be found using Pythagoras so we take the square root of v x squared plus v y squared so that's the square root of 9.8 squared plus 6.4 squared giving us 11.7047. And then the angle here Θ we'll use tangent of Θ is the opposite over the adjacent so that's the length of v y 6.40 divided by length of v x which is 9.8 and so we are using the inverse tangent here to find the angle Θ and that gives 33.1 degrees below the positive x-axis and then the magnitude is 11.70 units. So we have four significant figures there because this number here has three significant figures but it's precise to the hundredths place and this also is precise to the hundredths place and so the answer is precise to the hundredths place which turns out to have four significant figures. And this has three significant figures each and you know, there's more sophisticated ways of making estimates of significant figures but you know, let's just apply the same division rule as we would to this inverse tangent and then we'll get 33.1 is our answer here—three significant figures.