
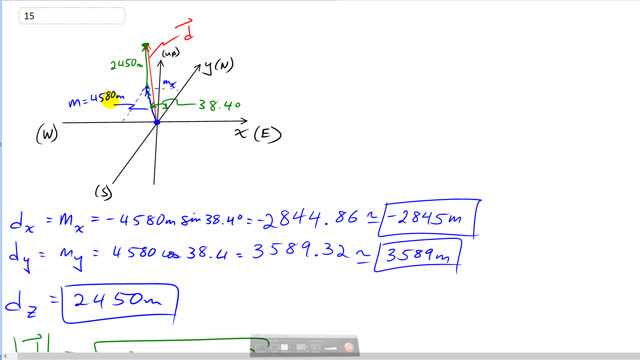
The summit of a mountain, 2450 m above base camp, is measured on a map to be 4580 m horizontally from the camp in a direction west of north. What are the components of the displacement vector from camp to summit? What is its magnitude? Choose the x axis east, y axis north, and z axis up.
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. On the map, horizontally, which means in the plane of north and east we have a distance to the summit of 4580 meters. So that's somewhat to the west and somewhat to the north and that's not including any upwards direction. We are told separately that it's upwards 2450 meters above where the base camp is so base camp is here. So this is in 3D and this line connecting the base camp to a point directly below the summit is 38.4 degrees to the west of north. Now, the x-component of the resultant vector which is this red one—d— connecting the base camp directly to the summit is gonna be the same as the x-component of the vector on the map and the plane on the map. And so that's 4580—and it's negative because it's to the west—meters times sin of 38.4 because it's the opposite leg of this triangle here and we get negative 2845 meters is the x-component of this displacement to the summit from the base camp. And the y-direction, we are gonna find this component of the vector and that's 4580 times cos of 38.4 because it's the adjacent leg of this triangle here and that gives 3589 meters. And then the z-component is the easiest one to find because we are told that directly that it's 2450 meters directly above or not directly above but anyway, it's 2450 meters higher than the base camp. The length of this resultant is the sum of the squares of all three components square rooted. So we take the square root of the x-component squared plus the y-component squared plus the z-component squared and we get 5190 meters is the total distance to the summit from base camp.