
Determine the vector , given the vectors and in Fig. 3-35.
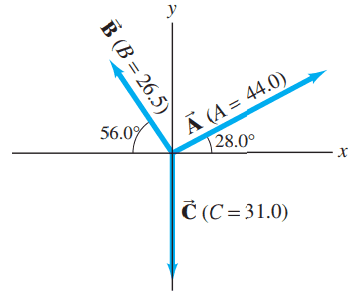
In order to watch this solution you need to have a subscription.
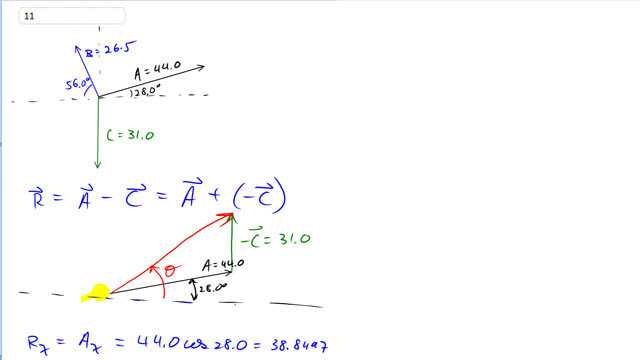
This is Giancoli Answers with Mr. Dychko. The way I like to think about subtracting vectors is adding the opposite because then you can use the head to tail method of adding vectors. So we have vector A which is redrawn here and on the head of vector A, you put the tail of the opposite of C so the opposite of C is this vector in the other direction, straight up in this case so we have the green one shown here. And then the resultant goes from the very beginning to the very end so that's drawn in red here. So we'll find the length of the resultant by finding its components first and then use Pythagoras and then use inverse tangent to get its angle and that's the usual routine for vectors. So the resultant x-component is the x-component of vector A because vector negative C has no x-component so we have 44 times cos 28 so length of vector A times cos of its angle here gives the x-component of the resultant and that's 38.8497 and then the y-component of the resultant will be the y-component of A that's this part here and that's found by taking the hypotenuse or length of A—44— and multiply by sin of 28; sin is the opposite divided by hypotenuse so when you multiply by the hypotenuse and then times by sin 28, you get the opposite and then add to that 31 and we get 51.657; I don't know, just in case, it's helpful to explain that a bit better we have sin 28, by definition, is opposite which in this case is y-component of A divided by hypotenuse which is A and then multiply both sides by A here and then A's cancel and then switch the sides around, you get A y is A times sin 28 and that's what we have put here and then we get 51.657 there and their resultant magnitude is the square root of the sum of the squares so square both of these components add them, take the square root and you get 64.6 units and then the angle Θ for the resultant is the opposite which is this length here— oops, it's going upwards though— so that's resultant y-direction that length divided by its x-component and so we get inverse tangent of 51.657 divided by divided by the x-component of 38.8497 and that gives 53.1 degrees and from the drawing, we can see that that's above the positive x-axis.