
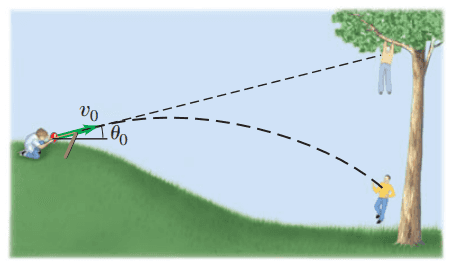
Revisit Example 3-7, and assume that the body with the slingshot is below the boy in the tree (Fig. 3-40) and so aims upward, directly at the boy in the tree. Show that again the boy in the tree makes the wrong move by letting go at the moment the water balloon is shot.
In order to watch this solution you need to have a subscription.
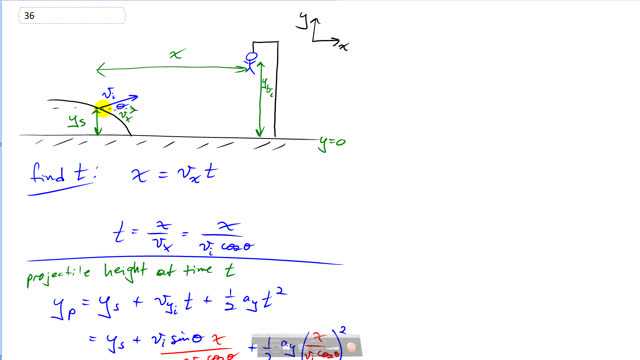
This is Giancoli Answers with Mr. Dychko. We are going to show that when this boy lets go of the tree, just at this moment the slingshot is fired that the projectile will hit the boy even though the projectile is being launched up at an angle Θ and starting at some height y S—for slingshot— below where the boy is; boy is at a height of y B—for boy; separation is this distance x and first we'll figure out at what time will this projectile be at this horizontal distance away from where it's launched and so this horizontal distance is x and it equals the horizontal component of the velocity, v x, multiplied by time and we know that v x is gonna be the initial velocity times cos Θ because v x is the adjacent leg of this velocity triangle here. And so the time when the projectile will be at the boy's horizontal position is the distance between the slingshot and the boy, x divided by v initial times cos Θ. And the next thing we'll figure out is what will the height of the projectile be at that time and then we'll compare that to the height of the boy at that time and if the height's are the same then that means there will be a collision. So we have the height of the projectile is the height of the slingshot initially plus the vertical component of the projectile's velocity times time plus one-half times the projectile's vertical acceleration times time squared and then we'll substitute for the time, that we figured out just before, based on the horizontal distance that it covers and so that's what I have written in red here and this by the way, the vertical acceleration is negative g as upwards is the positive direction and so vertical acceleration is negative g. And we'll substitute sin Θ over cos Θ as tan Θ— we don't really have to do that but it just looks a little bit more slick and the v i's cancel here and we have then at the height of the projectile, when it's at this horizontal position, is gonna be the initial height of the slingshot y S plus tan Θ times x minus g times x squared divided by 2 times initial velocity squared times cos squared Θ. So that's the projectile's height and then we'll figure out the boy's height at the same time. And the height of the boy then is the boy's initial height plus the initial y-component of the boy's velocity although there's none because he starts at rest at the tree and just lets go so that term disappears plus one-half at squared; well, a is negative g again and so we'll substitute for that and then time is the same time because the boy lets go at the same time as the slingshot is fired so we'll substitute an x over v i cos Θ for t and then that gets squared and so that's where this part comes from and this isn't quite looking the same as the height for the projectile although this last term is the same and so we know we are onto something; we need to change how this looks and if we can make this into this then we have shown that they are equal so that's our next task is to find a different way of expressing this initial height of the boy and we are gonna express it in terms of the height of the slingshot and we can use Θ as well. And we have this setup to begin with; we can create this triangle connecting the boy and the slingshot and they are separated by this distance x and this height here is the initial height of the boy and this is the height of the slingshot and we can say that tan Θ is this opposite leg of the triangle which is Δy—it's the difference between the boy's height and the slingshot's height— and divide it by the adjacent leg of the triangle which is x and that's what I have written here and then we'll multiply both sides by x because what we wanna do is solve for the initial height of the boy, we'll times both sides by x and we get the initial height of the boy minus the height of the slingshot equals x times tan Θ and then add height of the slingshot to both sides and we get initial height of the boy is y s plus x tan Θ. So when you substitute that in for the initial height of the boy here— that's what we have written here— then it becomes the same expression for the height of the projectile and so we have shown that the collision will happen because they have the same height at the same time.