
For the vectors shown in Fig. 3-35, determine
- ,
- .
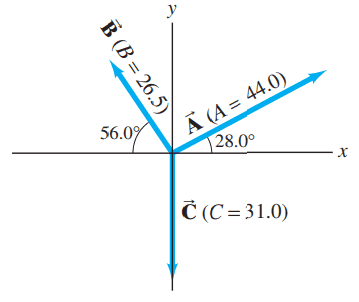
In order to watch this solution you need to have a subscription.
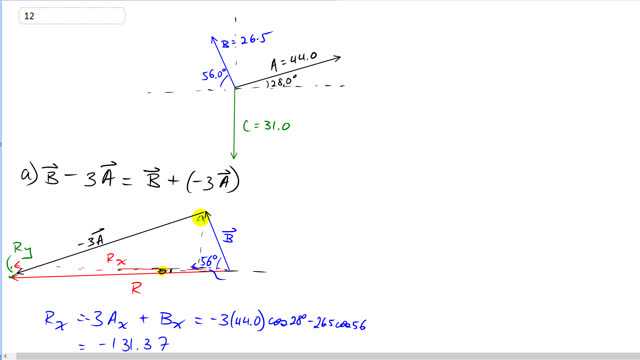
This is Giancoli Answers with Mr. Dychko. B minus 3A is the same as the vector B plus negative 3 times A and the reason I like to think of it that way is because you are still adding vectors so it's still the head to tail method and we put on the head of vector B— head of the first vector— we put the tail of the second vector and the second vector in this case is gonna be vector A but in the opposite direction, that's what the minus sign there means, and so here's negative 3A it's 3 times the length in the opposite direction and it's still 28 degrees but this time it's 28 degrees below the x-axis and our resultant will go from the very beginning which is at the tail of vector B to the very end which is the head of vector A or 3A I guess. The x-component of the resultant is gonna be the sum of the x-components of these vectors we are working with. So we have negative 3 times A x plus B x and the x-component of A is gonna be 44— it's length times the cos of 28— and then that's gonna be negative because it's to the left and then minus 26.5 which is the length of B times cos of 56 and that's a negative because it's to the left here and we get negative 131.37 is the x-component of the resultant and that's this part—starting from here all the way to here. And the y-component of the resultant is negative 3 times the y-component of vector A so it's negative 3 times 44 times sin 28 and then add to that the positive y-component of vector B— that's this portion right here— and the end result of that is negative 40 so there's a small y-component downwards for the resultant. And the length of the resultant then will be the square root of its x-component squared plus its y-component squared and so that gives 137.32 units and then the angle will be the inverse tangent of the opposite of R, its y-component and divided by the x-component of the resultant and that's 137.32 there and that gives 137 units, 16.9 degrees below the negative x-axis for the resultant there. In part (b), we have 2A so that's vector A in the same direction but 2 times the length and then plus negative 3B so that's vector B but in the down, to the right now 3 times the length and it's directed 56 degrees below the positive x-axis now and then plus 2C so vector C is straight down and it's twice the length so it's 62 units and 3 times B is 79.5 and 2 times A is 88. And then we get to work finding components and using Pythagoras to find the length of the resultant and use inverse tangent to get the angle, so I guess a little more slowly would be 2 times A x is 88 and then cos of 28 to get the x-component of that plus 79.5 is the length of 3B times the cos of 56 gives the x-component of B, that's this part just in here that's x-component of 3B and then there's no x-component for C so that's just zero and we have 122.155 is the x-component of the resultant and so that takes us this x-component of the resultant would be like this so that's R x. And then R y is this full part from down there and R y is found by going 2 times A y plus 3B y plus 2C y; y-component of A is upwards and so it's 88 times sin of 28 that's positive and this is the y-component of A right here 2A y I suppose and then we have plus 3B y now— this is in the downward direction so we put a minus sign in front of that— and so that's sin of 56 and that gives us the opposite here and times 79.5 and then minus 62—that's twice the length of C— that gives a negative 86.595. So the length of the resultant then is the square root of the x-component— 122.155—squared plus the y-component— negative 86.595—squared and that gives 149.7 units and then find the angle by going inverse tangent of the y-component divided by the x-component and then use the diagram to see that this is below the positive x-axis. So that's 35.3 degrees below the positive x-axis.
why is he not multiplying the 3 to the A in part A as he does in B. In B he doubles and triples the lengths of the sides.
Hi olever8, thanks for the question. In part A, the video shows the vector A length multiplied by 3, as expected. Perhaps what you're noticing is that I overlooked saying it was multiplied by 3 at one point, but the multiplying does indeed happen.